摘要:本文介绍了偶极子、偶极矩、诱导偶极矩、极性分子和非极性分子的相关概念,并以顺式和反式二氯乙烯为例,详细介绍了如何利用Gaussian程序计算分子偶极矩,并与实验测量的偶极矩对比,用来判断分子构型。
作者:陈宇
时间:2019-12-28
基本概念
电偶极子(Electric Dipole)
分别带有+q和-q电量,并且相距L的两个点电荷构成了一个电偶极子。
偶极矩(Dipole Moment)
偶极矩是描述电荷分布的一个物理量,它是一个矢量,用μ表示。对于只由两个点电荷组成的电偶极子,偶极矩的方向由负电荷指向正电荷,数值为电量q乘以距离L(μ=q*L)。 偶极矩的国际单位为C·m,然而很多情况,人们仍然使用D作为单位(以物理化学家Peter Debye命名)。其换算关系为:
1 D = 3.33564 × 10−30 C·m
对于分子体系,可以利用简单的经验模型,由不同化学键的偶极矩经过矢量加和得到整个分子的偶极矩,而通过量子化学计算,我们可以获得空间各点的电子密度,再经由计算得到整个分子的偶极矩。分子的对称性(广义的说就是原子的空间分布)和成键原子的电负性共同决定了分子的偶极矩。
极性分子(Polar Molecules)
具有永久偶极矩的分子就称为极性分子,对于极性分子,其正电中心和负电中心没有重合在一点,因此产生了永久偶极矩。
非极性分子(Nonpolar Molecules)
不具有永久偶极矩的分子就是非极性分子,对于非极性分子,其正电中心和负电中心重合在一点。
诱导偶极矩(Induced Dipole Moment)
非极性分子虽然不具有永久偶极矩,然而在外电场(或其他极性分子)的作用下,电子与原子核的相对位置能够发生改变,导致正电中心和负电中心不再重合,从而产生偶极矩,这种偶极矩称为诱导偶极矩。一旦移除外加电场,诱导偶极矩就会消失。对于极性分子,在外加电场作用下也会产生诱导偶极矩。
利用Gaussian程序计算分子偶极矩(Dipole Moment)的流程
由于分子偶极矩与分子的极性和分子构型有密切的关系,因此通过计算偶极矩,我们能够对判断与分子极性相关的理化性质,以及分子构型提供帮助。Gaussian程序在结构优化或单点能计算任务结束后会自动进行偶极矩的计算(也包括多极矩,例如四极矩,八极矩和十六极矩)。
计算偶极矩的基本流程:
- 结构优化
- 偶极矩计算
- 结果分析
首先优化分子结构,寻找能量最低的构象。
使用优化好的分子作为初始结构,用更大的基组进行偶极矩计算。
我们提到,分子的极性和构型与分子偶极矩密切相关,因此我们能够通过计算分子的偶极矩来判断特定分子的极性。此外通过计算分子不同构型的偶极矩,并且与实验值比较,我们也能够判断分子的构型。
算例

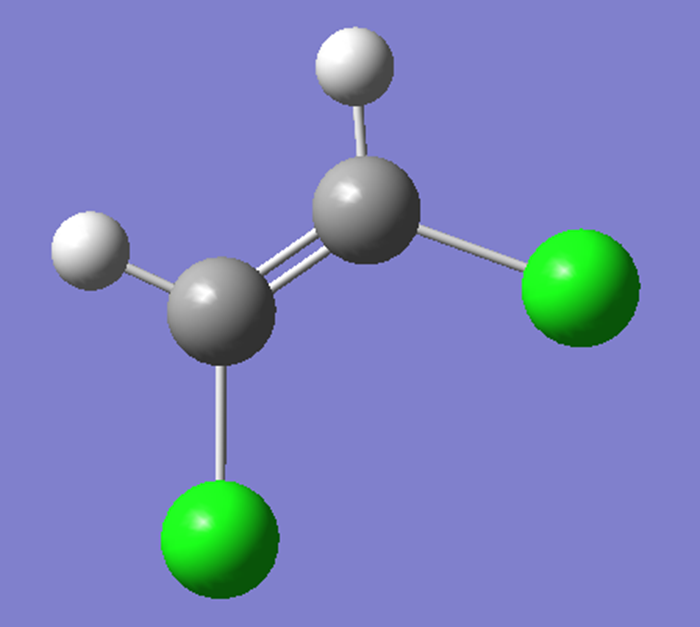
Figure 1. 算例化合物1,2-二氯乙烯:顺式(左),反式(右)
在本文中,我们以二氯乙烯作为例子,计算气相条件下顺式和反式二氯乙烯的偶极矩,通过对计算结果的分析,我们希望对下面两个问题做出解答:
- 顺式和反式二氯乙烯是极性分子还是非极性分子?
- 如何通过比较实验测得的和计算获得的顺式和反式二氯乙烯偶极矩来判断测试样品的分子构型?
1. 优化顺式(Z)和反式(E)1,2-二氯乙烯的结构
顺式(Z)二氯乙烯结构优化,Gaussian输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | %mem=1GB %nproc=8 # apfd/6-31G(d) opt freq Z-opt 0 1 C -0.56017395 0.54293784 0.00000000 H -0.02701020 -0.38476708 0.00000000 C 0.11510036 1.71791514 0.00000000 H 1.18510036 1.71791514 0.00000000 Cl -0.76187926 3.24385968 0.00000000 Cl -2.32017395 0.54293784 0.00000000 !空白行都是特意留出,不可删除 |
反式(E)二氯乙烯结构优化,Gaussian输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | %mem=1GB %nproc=8 # apfd/6-31G(d) opt freq E-opt 0 1 C -0.56017395 0.54293784 0.00000000 H -0.02701020 -0.38476708 0.00000000 C 0.11510036 1.71791514 0.00000000 Cl -2.32017395 0.54293784 0.00000000 H -0.41806339 2.64562006 0.00000000 Cl 1.87510036 1.71791514 0.00000000 !空白行都是特意留出,不可删除 |
2. 用不同基组计算顺式(Z)和反式(E)1,2-二氯乙烯的偶极矩
使用第一步优化得到的结构作为初始结构,计算顺式和反式二氯乙烯在不同方法基组下的偶极矩。我们尝试了四种不同的方法基组组合,分别如下:
1 2 3 4 | apfd/6-31G(d) apfd/6-311+G(d,p) apfd/6-311++G(3df,2p) m062x/6-311++G(3df,2p) |
下面我们给出顺式和反式二氯乙烯在apfd/6-311+G(d,p)水平下计算偶极矩的输入文件,其他方法基组下的计算只需用选用的方法基组替换即可。
顺式二氯乙烯在apfd/6-311+G(d,p)水平下计算偶极矩的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | %mem=1GB %nprocshared=8 # apfd/6-311+G(d,p) Z-Dipole 0 1 C -1.09239600 0.40390200 0.00000000 H -2.07755800 0.85918300 0.00000000 C 0.00000000 1.16464500 0.00000000 H -0.08569700 2.24654300 0.00000000 Cl 1.61529800 0.57828800 0.00000000 Cl -1.10249600 -1.31458300 0.00000000 !空白行都是特意留出,不可删除 |
实际上,这只是进行一个单点能计算,即可获得偶极矩的计算值。
反式二氯乙烯偶极矩计算的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | %mem=1GB %nprocshared=8 # apfd/6-311+G(d,p) E-Dipole 0 1 C -0.36598400 0.55478200 0.00000000 H -1.45060900 0.56101400 0.00000000 C 0.36598400 -0.55478200 0.00000000 Cl 0.36598400 2.11891600 0.00000000 H 1.45060900 -0.56101400 0.00000000 Cl -0.36598400 -2.11891600 0.00000000 !空白行都是特意留出,不可删除 |
3. 用GaussView查看结果
利用GaussView查看分子偶极矩的大小和方向,我们以顺式二氯乙烯为例,方法如下:
GaussView 6| File |Open 读入Gaussian的计算结果文件(.log):
在GussView 6 | Results下拉菜单中点击Charge Distribution选项,将显示与分子电荷相关的性质:
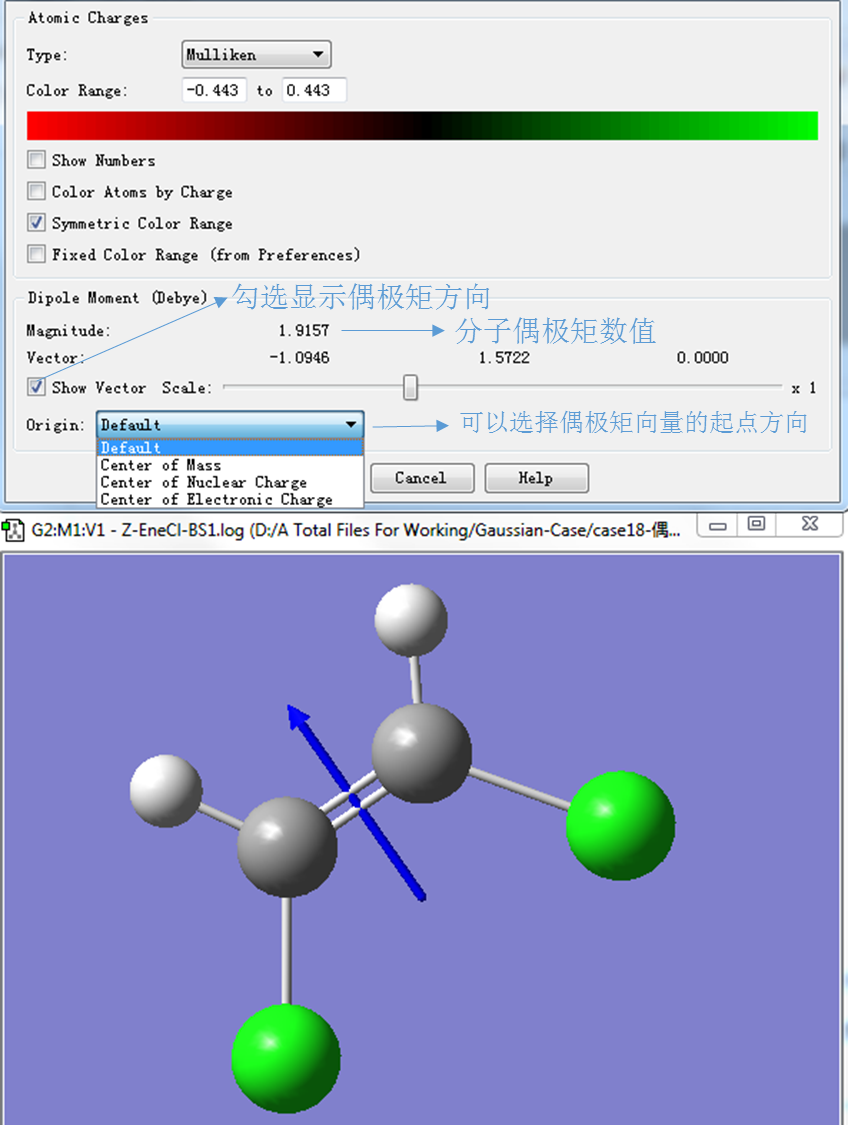
在Charge Distribution对话框,我们可以通过勾选Show Vector Scale显示偶极矩的方向。此外,通过选择origin的选项,我们能够调整向量的起点。
4. 结果分析
利用同样的方法我们可以查看顺式和反式构型在不同方法基组下的偶极矩数值,表1列出了顺式和反式构型在不同方法基组下的偶极矩数值。从表1可以看出在这个例子中,反式二氯乙烯的偶极矩均为零,表明反式二氯乙烯是非极性分子;而顺式二氯乙烯的偶极矩不为零,这说明顺式二氯乙烯是极性分子。因此通过对比实验值测量值,我们能够容易的判断分子的构型取向,尽管这个例子中我们通过分子对称性就可以判断反式二氯乙烯偶极矩为零,但对于其他更为复杂的极性分子,就需要比较偶极矩的大小才能够进行判断。
Table 1. 不同基组计算的偶极矩
| apfd/6-31g(d) | apfd/6-311+g(d,p) | apfd/6-311+g(3df,p) | apfd/6-311++g(3df,p) | |
|---|---|---|---|---|
| 顺式二氯乙烯 | 2.0319 | 1.9157 | 1.8415 | 1.8885 |
| 反式二氯乙烯 | 0.0 | 0.0 | 0.0 | 0.0 |
注意事项
需要注意的是:外加电场会使分子产生诱导偶极矩,因此溶剂会对偶极矩产生影响,在研究过程需要考虑;同时,方法和基组的选择对偶极矩的计算数值也有较大影响,在研究过程中也需要考虑。
参考资料
- Exploring Chemistry with Electronic Structure Methods, 3rd ed., Gaussian, Inc.: Wallingford, CT, 2015. J. B. Foresman and Æ Frisch
- ATKINS’ PHYSICAL CHEMISTRY



