摘要：在2004年，化合物Nankakurine A(15a)被首次分离出来，根据NOE与NMR数据将螺原子中心的构型确认为15b。在2006年，同一课题组重新将这个化合物修正为15a。在2008年，Overman课题组全合成了化合物15a与15b, 发现15a与Nankakurine A更匹配。Goodman课题组用计算NMR法将Nankakurine A归属为15a。作为演示DP4概率计算的算例，我们尝试将15a的实验数据归属为两个候选结构15a和15b之一，并用R与Python重现了Goodman课题组DP4概率的计算过程。

作者：肖高铿
日期：2020/10/10
修订（2020/10/12）： 根据后期的DP4-AI代码，修改了校正误差的计算方法，虽然并不能重现原文的DP4值，但是与DP4-AI计算方法一致。

关于DP4概率的算例

Kobayashi课题组在2004年时分离出化合物Nankakurine A(图1，15a)，根据NOE与NMR数据将螺原子中心的构型确认为15b[1]。在2006年的时候，该课题组根据分离到的相关化合物，重新将这个化合物确认为15a[2]。在2008年的时候，Overman课题组[3]全合成了化合物15a与15b, 发现15a与之前发现天然产物更匹配。

DP4概率的计算-墨灵格的博客

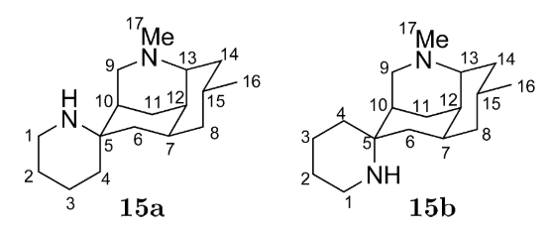
Figure 1. 算例化合物Nankakurine A的两个潜在异构体

Goodman课题组[4]提出的DP4概率常用于辅助差向异构体的立体化学结构解释。DP4专为以下情况而设计：根据一个未知化合物的NMR数据，将其从两个或更多可能的结构归属为其中一个。作为演示DP4计算方法的算例，我们尝试将天然产物（15a）的实验数据归属为两个候选结构15a和15b之一。 我们也可以考虑其他非对映异构体，但是在此示例中，假设可以通过耦合常数和NOE分析可靠地指定刚性笼结构中六元环的立体化学，因此仅仅是螺中心原子的构型需要进一步确定。

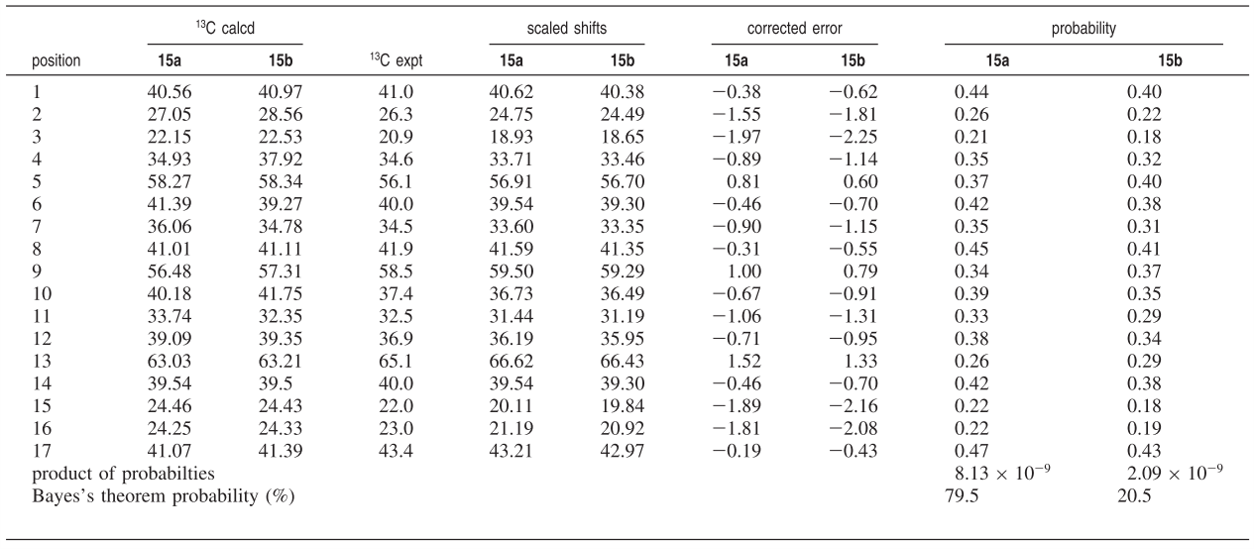
Table 1. 算例化合物Nankakurine A的DP4分析（来自原文Table 2[4]）

DP4概率的计算-墨灵格的博客

化合物Nankakurine A(图1)两个异构体用Gaussian软件GIAO NMR计算的13C NMR化学位移(15a)、实验化学位移以及DP4计算中间过程数据与结果见表1。作者计算的15a与15b的DP4概率分别为79.5%与20.5%，接下来我们尝试用R与Python重现该计算结果。

准备工作

首先，你需要先阅读Smith与Goodman[4]关于DP4概率计算的原文，理解DP4的算法；其次，你需要安装R软件包或Python。

用R计算DP4概率流程(t-分布法)

1. 输入计算值与实验值

按照原文Table2，将算例化合物的两个异构体(15a，15b)计算的13C NMR数据与实验的13C NM数据以数组的方式输入，分别为C13.15a,C13.15b,C13.exp：

1
2
3

C13.15a <-c(40.56, 27.05, 22.15, 34.93, 58.27, 41.39, 36.06, 41.01, 56.48, 40.18, 33.74, 39.09, 63.03, 39.54, 24.46, 24.25, 41.07)
C13.15b <-c(40.97, 28.56, 22.53, 37.92, 58.34, 39.27, 34.78, 41.11, 57.31, 41.75, 32.35, 39.35, 63.21, 39.50, 24.43, 24.33, 41.39)
C13.exp <-c(41.0, 26.3, 20.9, 34.6, 56.1, 40.0, 34.5, 41.9, 58.5, 37.4, 32.5, 36.9, 65.1, 40.0, 22.0, 23.0, 43.4)

2. 拟合计算值与实验值

分别将15a与15b的计算值与实验值进行拟合：

1
2

fit.15a  <- lm(C13.15a ~ C13.exp)
fit.15b  <- lm(C13.15b ~ C13.exp)

3. 计算scaled化学位移

也就原文Table 2的scaled shift，需要先创建个scale函数：

1
2
3

scale.calc <- function(x,y,z) {a  <- (x - y)/z
return(a)
}

其中x为计算的化学位移，y为回归方程的截距(intercept); z为回归方程的斜率(slope)。

用初始的预测值计算scaled化学位移：

1
2

Scaled.15a  <- scale.calc(C13.15a,fit.15a$coefficients[[1]],fit.15a$coefficients[[2]])
Scaled.15b  <- scale.calc(C13.15b,fit.15b$coefficients[[1]],fit.15b$coefficients[[2]])

4. 计算校正误差(Corrected error)

现在计算Table 2的corrected error。根据DP4-AI的文章与源代码[5,6]，校正误差应该为Scaled的计算值减去实验值:

1
2

Corr.15a  <- Scaled.15a - C13.exp
Corr.15b  <- Scaled.15b - C13.exp

5. 计算DP4概率

鉴于原文采用学生氏t分布（The Student t Distribution）计算概率，而且在作者Goodman课题组[7]网站的DP4计算教程中也认为t-分布更合适：

DP4 can be calculated assuming either a normal distribution or a t-distribution for the error in any individual calculated shift. We recommend using the t-distribution because we have found that it is less susceptable to overstating the probability. However, you can choose to carry out the calculation using the normal distribution of you wish. More information can be found in the journal article on DP4 (manuscript submitted).

因此这里采用R的pt模块来计算概率：

1
2
3
4

prob  <- function(x,sigma=2.306,nu=11.38) {
y  <- 1-pt((abs(x)/sigma),nu)
return(y)
}

13C-NMR的sigma=2.306与nu=11.38，取自Smith[4]的附件S4。应该要注意不同的DP4版本这两个值可能会不同，比较DP4概率值的时候应该要注意使用的是哪个版本。

Table 2. μ与σ值(来自Smith[4]的S4)

C H
μ/ppm 0 0
σ/ppm 2.306 0.185
ν/ppm 11.38 14.18


用概率函数计算每个原子的校正误差概率（也就是表1的probability列）：

1
2

Prob.15a  <- prob(Corr.15a)
Prob.15b  <- prob(Corr.15b)

现在可以根据原文方程（3）计算15a的DP4概率：

1
2

DP4.15a <- 100*prod(Prob.15a)/(prod(Prob.15a)+prod(Prob.15b))
DP4.15a
1

[1] 90.31366

计算15b的DP4概率：

1
2

DP4.15b <- 100*prod(Prob.15b)/(prod(Prob.15a)+prod(Prob.15b))
DP4.15b
1

[1] 9.686337

6. 小结

原文15a与15b的DP4概率分别为79.5%与20.5%，而本次计算的DP4分别为90.3%与9.7%，两者在数值上有较大的差异，但是对结构的归属不产生影响。

用Python计算DP4概率流程(正态分布法)

1. 加载必要软件包

1
2

from scipy import stats
import numpy as np

2. 加载DP4-AI的标准参数

加载概率计算的参数，来源于DP4-AI[5]（2020-10-10访问）。该参数是经验参数，可能会随不同版本变化而变化。

1
2
3
4
5

# Standard DP4 parameters
meanC = 0.0
meanH = 0.0
stdevC = 2.269372270818724
stdevH = 0.18731058105269952

3. 输入计算值与实验值

1
2
3

C13_15a = [40.56, 27.05, 22.15, 34.93, 58.27, 41.39, 36.06, 41.01, 56.48, 40.18, 33.74, 39.09, 63.03, 39.54, 24.46, 24.25, 41.07]
C13_15b = [40.97, 28.56, 22.53, 37.92, 58.34, 39.27, 34.78, 41.11, 57.31, 41.75, 32.35, 39.35, 63.21, 39.50, 24.43, 24.33, 41.39]
C13_exp = [41.0, 26.3, 20.9, 34.6, 56.1, 40.0, 34.5, 41.9, 58.5, 37.4, 32.5, 36.9, 65.1, 40.0, 22.0, 23.0, 43.4]

4. 计算scaled化学位移

1
2
3
4

def ScaleNMR(calcShifts, expShifts):
    slope, intercept, r_value, p_value, std_err = stats.linregress(expShifts,calcShifts)
    scaled = [(x - intercept) / slope for x in calcShifts]
    return scaled
1
2

scaled_15a = ScaleNMR(C13_15a, C13_exp)
scaled_15b = ScaleNMR(C13_15b, C13_exp)

5. 计算校正误差(Corrected error)

根据DP4-AI的文章与源代码[5,6]，校正误差应该为Scaled的计算值减去实验值:

1
2
3

import numpy as np
err_15a = list(np.array(scaled_15a) - np.array(C13_exp))
err_15b = list(np.array(scaled_15b) - np.array(C13_exp))

注：为了重现原文Table2的结果，将校正误差计算方法进行修改：

1
2
3

import numpy as np
err_15a = list(np.array(scaled_15a) - np.array(C13_15a))
err_15b = list(np.array(scaled_15b) - np.array(C13_15b))

但这样与原文附录的计算方法描述不相符。

6. 计算DP4概率

用概率函数计算每个原子的校正误差概率（也就是表1的的probability列）：

1
2
3
4

def SingleGausProbability(error, mean, stdev):
    z = abs((error - mean) / stdev)
    cdp4 = 2 * stats.norm.cdf(-z)
    return cdp4
1
2
3
4
5
6
7
8
9

Prob_15a = []
for e in err_15a:
    cdp4 = SingleGausProbability(e, meanC, stdevC)
    Prob_15a.append(cdp4)
 
Prob_15b = []
for e in err_15b:
    cdp4 = SingleGausProbability(e, meanC, stdevC)
    Prob_15b.append(cdp4)

创建概率乘积函数：

1
2
3
4
5

def multiplyList(myList):
    product = 1
    for x in myList:
        product = product * x 
    return product

计算15a的DP4概率（Bayes’s theorem probability, %）：

1
2

dp4_15a =  100*multiplyList(Prob_15a)/(multiplyList(Probs_15a)+multiplyList(Probs_15b))
print(dp4_15a)
1

92.66701404998044

计算15b的DP4概率（Bayes’s theorem probability, %）：

1
2

dp4_15b =  100*multiplyList(Prob_15b)/(multiplyList(Probs_15a)+multiplyList(Probs_15b))
print(dp4_15b)
1

7.332985950019572

7. 小结

本次计算结果表明，15a与15b的DP4概率分别为92.7%与7.3%，这与作者的报道的79.5%与20.5%差值巨大，但是不影响对绝对构型的判断。

其它回归评估统计学指标的计算

其它的常用评价指标包括线性相关性、均方误差（MSE）、均方根误差（RMSE）与平均绝对误差（MAE）。假设, ýi表示预测值；yi表示实验值，则MSE、RMSE与MAE计算方法如下：

  • Pearson相关性系数(Pearson correlation coefficient)

    • Pearson相关性系数用于评价两组数据的线性相关性，跟多的细节请查阅Scipy手册。该系数范围[-1,1]，系数等于0时表示没有相关性；系数为-1或1表示完美的线性相关。

  • 均方误差(Mean Square Error)
    • DP4概率的计算-墨灵格的博客

    MSE范围[0,+∞)，MSE=0表示模型完美，预测值与真实值完全吻；MSE越大，误差越大。

  • 根均方误差(Root Mean Square Error)
    • DP4概率的计算-墨灵格的博客

    RMSE是MSE的开方根，范围[0,+∞)，RMSE=0表示模型完美，预测值与真实值完全吻合；RMSE越大，误差越大。

  • 平均绝对误差（Mean Absolute Error）
    • DP4概率的计算-墨灵格的博客

    范围[0,+∞)，RMSE=0表示模型完美，即预测值与真实值完全吻合；RMSE越大，误差越大。

Scaled预测值与实验值的Pearson相关性系数计算

15a的Pearson相关性系数与p值计算如下：

1
2
3

import scipy.stats as stats
r, p_value = stats.pearsonr(C13_exp, scaled_15a)
print(r,p_value)
1

0.9932022991772373 1.988951666126653e-15

15b的Pearson相关性系数与p值计算如下：

1
2
3

import scipy.stats as stats
r, p_value = stats.pearsonr(C13_exp, scaled_15b)
print(r,p_value)
1

0.9901344309365251 3.2210035705008464e-14

Scaled预测值与实验值的MSE与RMSE计算

15a的MSE与RMSE计算如下：

1
2
3
4

from sklearn.metrics import mean_squared_error
mse = mean_squared_error(C13_exp, scaled_15a)
rmse = mse**0.5
print(mse,rmse)
1

2.024510252561101 1.422852856960656

15b的MSE与RMSE计算如下：

1
2
3
4

from sklearn.metrics import mean_squared_error
mse = mean_squared_error(C13_exp, scaled_15b)
rmse = mse**0.5
print(mse,rmse)
1

2.951876716914859 1.7181026502845687

Scaled预测值与实验值的MAE计算

15a的MAE计算如下：

1
2
3

from sklearn.metrics import mean_absolute_error
MAE = mean_absolute_error(C13_exp, scaled_15a)
print(MAE)
1

1.1793885437445262

15b的MAE计算如下：

1
2
3

from sklearn.metrics import mean_absolute_error
MAE = mean_absolute_error(C13_exp, scaled_15b)
print(MAE)
1

1.417549405035919

讨论

无论是根据学生氏t-分布的计算方法，还是根据DP4-AI里的Gaussian分布计算方法，两者的DP4概率值基本一致：前者计算的15a/15b的DP4概率分别为90.3%与9.7%，后者计算15a/15b的DP4概率分别为92.7%与7.3%。但都与原文的DP4概率79.5%与20.5%差值较大。为了考察是否计算出错，还用DP4-AI的IP4算例进行验证，了比较本文方法与DP4-AI方法的DP4计算结果，结果发现可以本文方法与DP4-AI计算结果是一致的，因此本文的计算方法上不存在任何问题。

下载Jupyter notebook

下载地址：https://github.com/gkxiao/DP4

相关教程

DP4-AI全自动DP4概率计算：DP4-AI的使用。

文献

  1. Hirasawa, Y.; Morita, H.; Kobayashi, J. Nankakurine A, a Novel C 16 N 2 -Type Alkaloid from Lycopodium h Amiltonii. Org. Lett. 2004, 6 (19), 3389–3391. https://doi.org/10.1021/ol048621a.
  2. Hiroshi Morita, Yusuke Hirasawa, Jun’ichi Kobayashi, Yutaro Obara, Norimichi Nakahata, Nobuo Kawahara, Yukihiro Goda. Nankakurine B, a New Alkaloid from Lycopodium hamiltonii and Revised Stereostructure of Nankakurine A. HETEROCYCLES 2006, 68 (11) , 2357. https://doi.org/10.3987/COM-06-10868
  3. Bradley L. Nilsson, Larry E. Overman, Javier Read de Alaniz and Jason M. Rohde. Enantioselective Total Syntheses of Nankakurines A and B: Confirmation of Structure and Establishment of Absolute Configuration. Journal of the American Chemical Society 2008, 130 (34) , 11297-11299. https://doi.org/10.1021/ja804624u
  4. Smith, S. G.; Goodman, J. M. Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability. J. Am. Chem. Soc. 2010, 132 (37), 12946–12959. https://doi.org/10.1021/ja105035r.
  5. DP4-AI. https://github.com/KristapsE/DP4-AI
  6. Howarth, A.; Ermanis, K.; Goodman, J. M. DP4-AI Automated NMR Data Analysis: Straight from Spectrometer to Structure. Chem. Sci. 2020, 11 (17), 4351–4359. https://doi.org/10.1039/D0SC00442A.
  7. Goodman. How do I calculate DP4?. http://www-jmg.ch.cam.ac.uk/tools/nmr/DP4/instructions.html

联系我们