摘要：本文以Fenchol及其对映异构体Alt-Fenchol为例，演示了如何用ORCA计算其VCD图谱，并用Cai Factor来自动解释VCD图谱，并评估绝对构型指认的置信度。ORCA与Cai•factor联合使用是高效的VCD结构确证计算工具。

肖高铿/2024-09-04

前言

振动圆二色谱（vibrational circular dichroism，VCD）是一种手性光谱技术，常用于化合物绝对构型的指认，然而该光谱却难以解释。为了解决这个问题，剑桥大学的Lam等人1提出了Cai•factor方法，用来自动分析VCD图谱并指认绝对构型。在一个包含有30对有机小分子VCD图谱的基准数据集上，Cai•factor方法的绝对构型指认表现可靠且高效，即使光谱不完美，它也能给出确定结果以及对结果的置信度评估指标。大多数测试的分子具有高置信度分数，并且所有这些分子都有正确的指认结果。

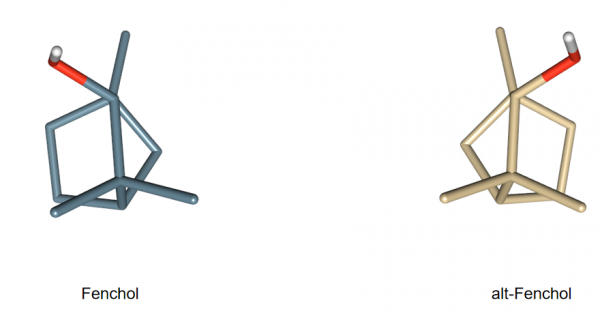
Fenchol与其对映异构体alt-fenchol的化学结构

图1. 对映异构体Fenchol与alt-fenchol的化学结构

ORCA 6.0是量子化学计算软件ORCA2,3,4的最新版本，该版本新增的一个功能是支持HF和DFT计算VCD图谱。本文的主要目的是，以如图1所示的Fenchol与alt-fenchol这一对对映异构体为例，演示如何用ORCA 6.0来计算VCD图谱，并用Cai•factor来进行图谱绘制，归属绝对构型，并评估对绝对构型指认的置信度。

材料与方法

构象分析

用Flare对化合物Fenchol构象搜索，然后用Flare QM在B3LYP/6-311+G(d,p)理论水平进行几何优化，得到三个不重复的构象：

struct
├── CONF_01.xyz
├── CONF_02.xyz
└── CONF_03.xyz

具体的操作过程请参见前文5：鸡蛋花素的ECD光谱计算，这里不再叙述。

用ORCA 6计算VCD谱

以构象CONF_01为例，在B3LYP-D4/DEF2-TZVPP/Chloroform理论级别计算VCD光谱。

准备输入文件vcd.inp：

1
2
3
4
5
6

%PAL NPROCS 20 END
! FREQ B3LYP D4 DEF2-TZVPP CPCM(chloroform)
%FREQ
    DoVCD TRUE
END
* xyzfile 0 1 ../struct/CONF_01.xyz

其中，3-5可以合并为一行：

1
2
3
4

%PAL NPROCS 20 END
! FREQ B3LYP D4 DEF2-TZVPP CPCM(chloroform)
%FREQ DoVCD TRUE END
* xyzfile 0 1 ../struct/CONF_01.xyz

执行计算：

1
2

cd CONF_01
$orca_root/orca vcd.inp > CONF_1.out

计算大约8分钟完成：

1
2
3
4
5
6
7
8
9
10

Timings for individual modules:
 
Sum of individual times          ...      496.719 sec (=   8.279 min)
Startup calculation              ...        2.673 sec (=   0.045 min)   0.5 %
SCF iterations                   ...       12.591 sec (=   0.210 min)   2.5 %
Property integrals               ...      178.983 sec (=   2.983 min)  36.0 %
SCF Response                     ...      119.908 sec (=   1.998 min)  24.1 %
Property calculations            ...      182.565 sec (=   3.043 min)  36.8 %
                             ****ORCA TERMINATED NORMALLY****
TOTAL RUN TIME: 0 days 0 hours 8 minutes 17 seconds 505 msec

ORCA计算结果的预处理

相似的，ORCA计算之后得到三个结果文件：

1
2
3
4

orca_result
├── CONF_01.out
├── CONF_02.out
└── CONF_03.out

因为cai_2020_alpha.py是为schrodinger/Jargua与Gaussian而准备，因此需要将ORCA结果模仿为Gaussian结果文件：

1
2
3

ORCA_VCD2caifactor.py CONF_01.out CONF_01.log
ORCA_VCD2caifactor.py CONF_02.out CONF_02.log
ORCA_VCD2caifactor.py CONF_03.out CONF_03.log

这里的ORCA_VCD2caifactor.py是自编的，你不必为如何写python而烦恼。你只需要知道你的目标，现在可以借助qwen2等各种LLM用近乎自然语言的方式来轻松实现，将来会写一个专题介绍。

用Cai•factor进行图谱解释

然后准备Cai•factor的输入文件cai.input，内容如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

<Settings>
title: Fenchol
broadening: 5.0
minimum_wavenumber: 950.0
maximum_wavenumber: 1500.0
temperature: 298.0
defined_scaling_factor: 0.98
boltzmann_cutoff: 10.0
print_csv spectra scaling_factor summary
<Experiments>
./fenchol-vcd.exp.xy 
 
<Blank>
 
<Calculations>
./calculated
 
!This is a blank line

其中Experiments部分的fenchol-vcd.exp.xy是实验图谱，由两列组成，第一列是波长（nm），第二列是vcd信号强度；其中，Blank区应该放置空白溶剂的实验结果文件，在计算中作为基线，格式与实验图谱一致；其中Calcluations是指计算结果文件所在的目录，在这个计算里，三个.log文件都放在calculated目录里。现在可以键入如下命令开始自动解释图谱，计算cai•factor：

1

cai_2020_alpha.py cai.input

结果

根据Lam等人1之前的验证研究，Cai•factor表示了对绝对构型归属的信心水平。Cai•factor的具体阈值如下：

  • \(Cai•factor \lt10 \)

    • 难以得出结论，可能意味着谱图质量较低，要么因为噪声大信号弱，要么因为谱图中没有明显的峰。

  • \(10 \lt Cai•factor \lt 20 \)

    • 通常正确，但存在一些误导性的例子。对于基于两种对映体的分析，有两个Cai•factor为10的例子可能会误导分析，而基于单一对映体测量的有16个中有3个可能会误导。

  • \(20 \lt Cai•factor \lt 30 \)

    • 对于两种对映体和单一对映体的计算，所有的归属都是正确的，除了一个例外（04_limonene_bruker的Cai•factor为21，归属错误）。

  • \(30 \lt Cai•factor \lt 40 \)

    • 尽管计算和实验之间的视觉关系可能不是很接近，但仍然可以对归属有相当高的信心。

  • \(40 \lt Cai•factor\)

    • 视觉归属通常非常清晰，从而有高度的信心。

可以认为Cai•factor值在20以上时，对绝对构型的归属有一定的信心。在实际应用中，作者建议对20到30之间的结果持谨慎态度，而Cai•factor值在30以上时，可以有较高的信心认为绝对构型归属是可靠的。

在本实验中，对fenchol进行Cai•factor计算的结果如图2所示。

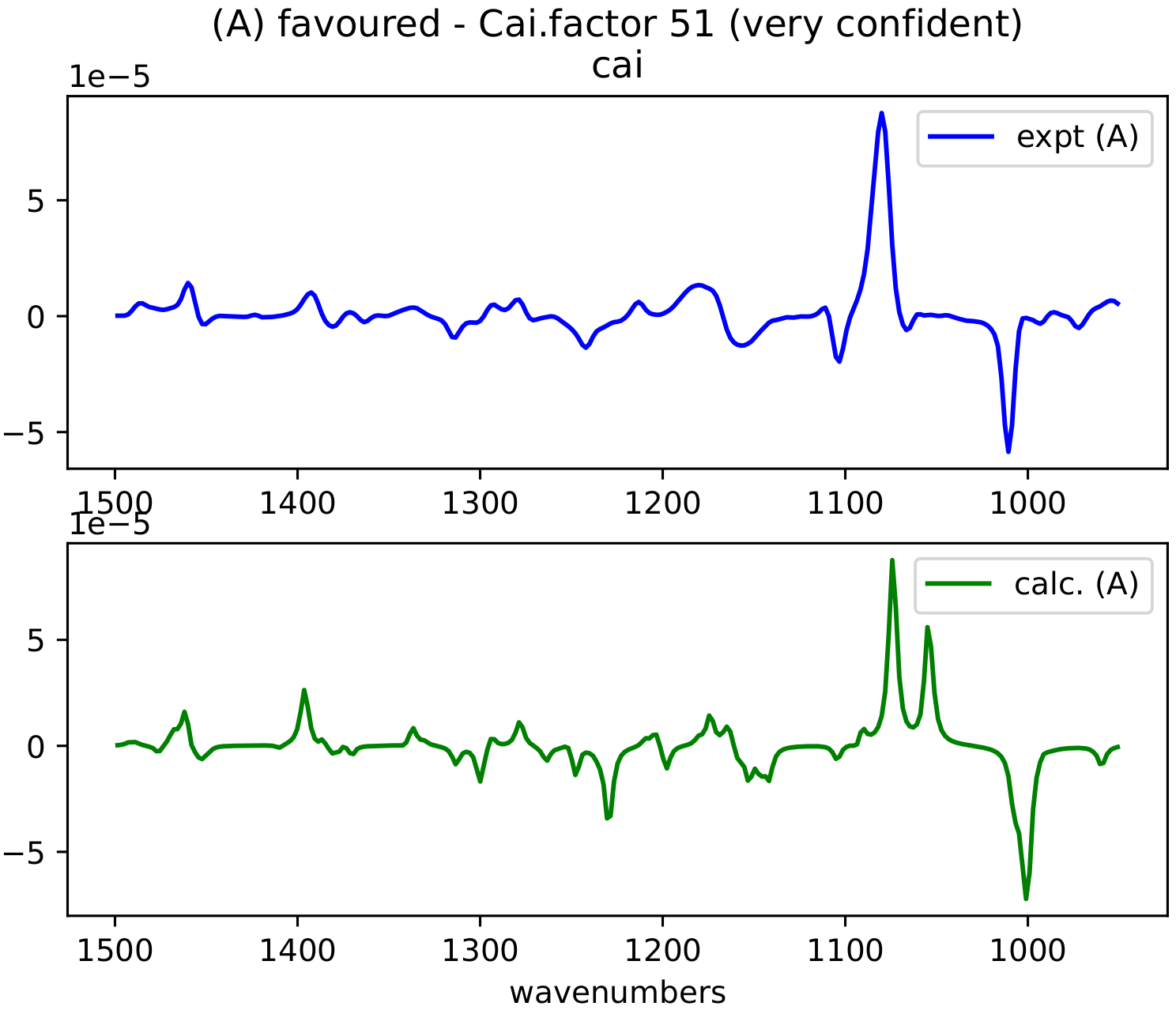
ORCA计算图谱与实验图谱的比较以及Cai因子

图2. ORCA计算fenchol的VCD图谱与实验图谱的比较以及Cai因子

我们可以发现计算的fenchol的VCD图谱与实验图谱非常相似，并且Cai•facotr=51，这远远地高于40，意味着可以高度信心认为绝对构型应该为fenchol，这个结论也与实际一致。

结论

在本文中以Fenchol及其对映异构体Alt-Fenchol为例，演示了如何用ORCA计算其VCD图谱，并用Cai Factor来自动解释VCD图谱，并评估绝对构型指认的置信度。结果表明，计算结果以高度的信心指认绝对构型为fenchol，并与实际一致。ORCA与Cai•factor联合使用是高效的VCD结构确证计算工具。

相关内容

文献

  1. Lam, J., Lewis, R.J. and Goodman, J.M. (2023) “Interpreting vibrational circular dichroism spectra: the Cai•factor for absolute configuration with confidence,” Journal of Cheminformatics, 15(1). Available at: https://doi.org/10.1186/s13321-023-00706-y.
  2. Neese, F. et al. (2020) “The ORCA quantum chemistry program package,” Journal of Chemical Physics, 152(22). Available at: https://doi.org/10.1063/5.0004608.

  3. Neese, F. (2022) “Software update: The ORCA program system—Version 5.0,” Wiley Interdisciplinary Reviews: Computational Molecular Science. Available at: https://doi.org/10.1002/wcms.1606.
  4. https://www.faccts.de/docs/orca/6.0/manual
  5. 鸡蛋花素的ECD光谱计算. http://blog.molcalx.com.cn/2024/04/23/plumericin-spectra-simulation.html

联系我们

我们提供一整套的结构确证解决方案，任何需要请联系我们。