摘要:本文介绍了电子自旋(spin)与自旋密度(spin density)等相关概念。并以(·CH2-CH2-CH2-CH2-CH2·)双自由基为例,详细介绍了如何利用Gaussian和GaussView计算、绘制分子的自旋密度图。
陈宇/2021-1-9
1 基本概念
1.1 电子自旋(Spin)
电子自旋(spin):自旋是微观粒子的基本性质,在量子力学中,人们使用自旋量子数来描述这个物理量。对于单电子而言,自旋量子数只存在两种可能的数值:1/2和-1/2。
1.2 自旋密度(spin density)
自旋密度:由于单电子只存在两种可能的自旋量子数,因此在量子化学计算中,我们将两种不同自旋量子数的电子区分为α电子和β电子,对于一个分子,其空间某点的电子自旋密度定义为这一点α电子密度和β电子密度的差:
ρ(自旋密度)= ρ(α电子密度) – ρ(β电子密度)
对于闭壳层体系,由于每一个α电子都有一个β电子与之配对,因此在空间的任意一点,α电子和β电子的密度都是相同的,也就意味着在空间各处自旋密度均为零。而对于开壳层体系,分为两种情况:当分子本身带有奇数电子时,由于一定存在一个未配对的α电子,因此一定有空间某点自旋密度不为零;当分子体系带有偶数电子时,若发生自旋极化,那么α电子和β电子轨道将不再完全重叠,此时空间某些区域的自旋密度也将不再为零。
在化学反应中,若分子的基态是自旋极化态,那么反应的活性位点往往处于自旋密度较高的区域;同样,自由基反应的位点也几乎都在自旋密度较高的区域,因此研究自旋密度的分布具有重要的价值。
关于开壳层的计算以及相关概念参见教程:Gaussian教程 | 模拟开壳层体系
2 绘制分子自旋密度
在本教程中,以(·CH2-CH2-CH2-CH2-CH2·)双自由基分子为例,详细介绍如何使用Gaussian和GaussView来绘制分子的自旋密度图。绘制分子自旋密度图的步骤包括:
- 优化分子结构
- 单点能计算
- 用GaussView绘制自旋密度图
使用优化好的分子作为初始结构,用更大的基组进行单点能计算,以获得分子基态的波函数。
2.1 优化分子结构
第一步要优化(·CH2-CH2-CH2-CH2-CH2·)双自由基的结构。输入文件如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | # opt freq ub3lyp/6-31g(d) guess=mix C5H10-Diradical 0 1 C 0.43527662 -0.43527665 0.00000000 C 1.94242662 -0.43527665 0.00000000 H 0.04174462 -0.95846765 -0.90491000 H 0.04165162 -0.95858165 0.90478800 H 2.31649362 0.62093375 -0.06466424 H 2.31656562 -0.85759975 0.97022527 C -0.10234233 1.00783314 0.00000000 C -1.60949232 1.00783314 0.00010303 H 0.29112781 1.53100109 -0.90495023 H 0.29134453 1.53116118 0.90474776 C -2.16923933 2.40716114 0.00003366 H -1.98362101 0.45509516 -0.90222532 H -1.98356963 0.45519612 0.90250668 H -3.28551133 2.38056514 0.00005265 H -1.82954619 2.96681909 -0.90489482 !所有空白行都是特意留出,不要忽略 |
其中第1行的guess=mix要求Gaussian程序在进行初始波函数猜测时破坏α/β电子的对称性,从而在单重态的计算中得到非限制性波函数。
2.2 用更大的基组进行单点能计算
使用第一步优化得到的结构作为初始结构,用UB3LYP/6-311G(d,p)进行一个单点能计算,并保留chk文件。输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | %chk=C5H10-diradical-SP.chk # ub3lyp/6-311g(d,p) guess=mix C5H10-Diradical-SP 0 1 C 1.29104200 0.50659600 -0.00035000 C 2.53365700 -0.30917100 0.00011500 H 1.26086200 1.16225800 0.88164000 H 1.26081600 1.16118100 -0.88312500 H 2.94001900 -0.70350700 0.92709100 H 2.94051100 -0.70371100 -0.92655100 C -0.00001000 -0.36137300 0.00017300 C -1.29102800 0.50659800 0.00029600 H 0.00019200 -1.01637700 0.88019400 H -0.00015100 -1.01691100 -0.87945000 C -2.53367600 -0.30915500 -0.00026200 H -1.26104200 1.16126400 0.88300000 H -1.26066200 1.16210500 -0.88180200 H -2.93973300 -0.70379400 -0.92723800 H -2.94072600 -0.70348900 0.92640600 !所有空白行都是特意留出,不要忽略 |
其中第1行%chk是保存check文件,以便用于后续生成自旋密度图。
2.3 使用GaussView绘制分子的自旋密度
首先,我们需要将生成的.chk文件转化为.fchk文件,才能够让GaussView读取。方法是在linux命令行输入:
[gkxiao@master demo]$ formchk filename.chk
其中formchk是命令,filename是要转化的文件名(需要加文件后缀,也就是.chk),敲击回车之后会生成一个filename.fchk文件。
将.fchk文件拖入GaussView中打开文件,然后在Results菜单下点击Surfaces/Contours选项,会出现如下图1的界面。
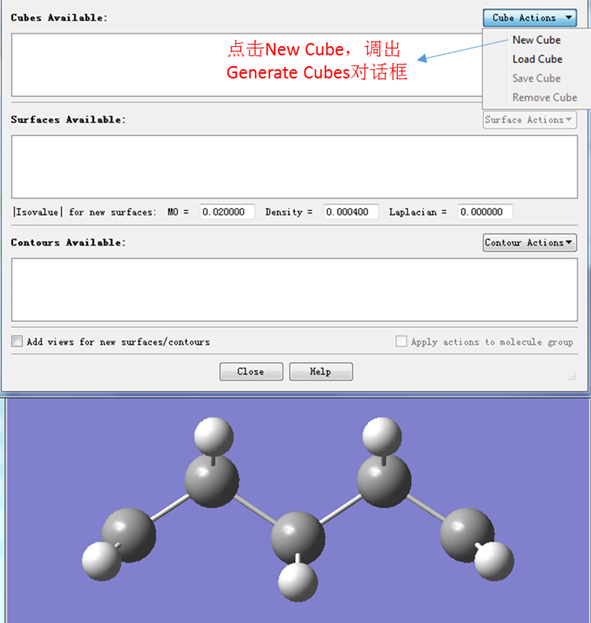
图1. Surfaces and Contours对话框
如图1所示,在Cube Actions下拉菜单中点击New Cube选项,会弹出Generate cubes对话框,如图2所示。
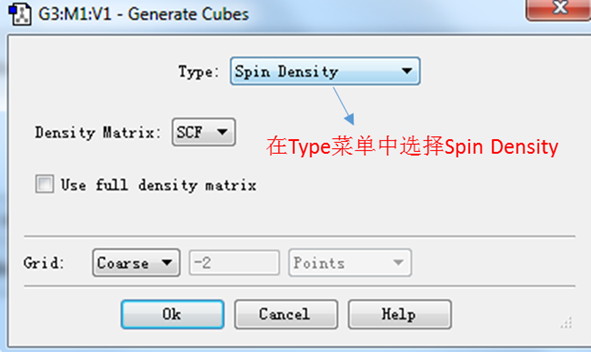
图2. Generate Cubes对话框
如图2所示,确保type下来选项里为Spin Density后,点击ok按钮。此时gaussian程序会开始进行计算,因此要确保电脑已经安装了gaussian程序包。当计算完成,Surfaces and Contours对话框的cubes available会更新:多出一行内容,如图3所示。
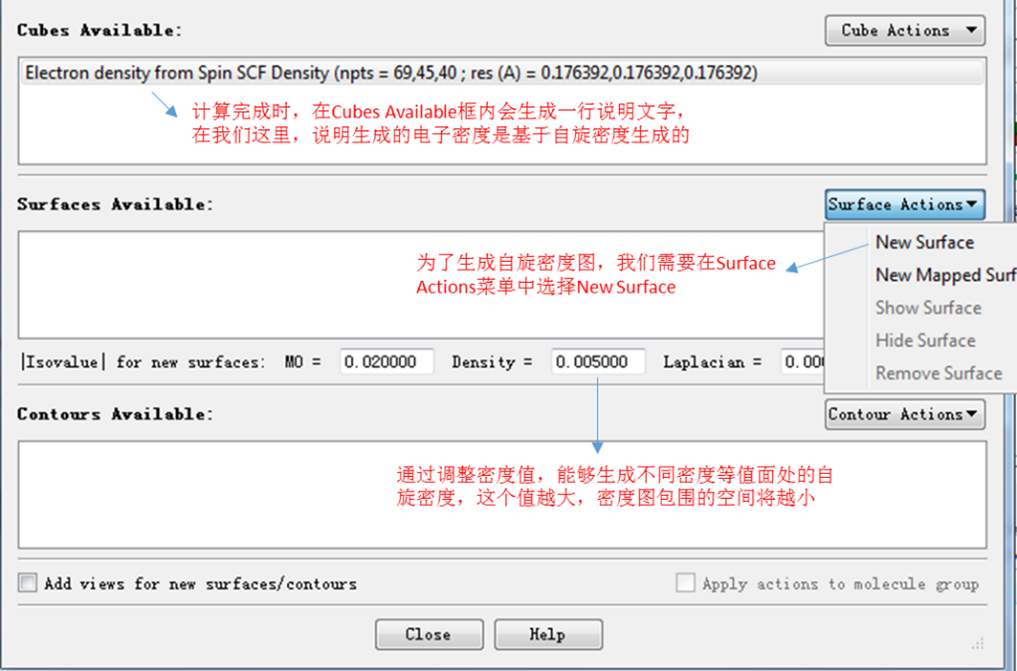
图3. Generate cubes完成Spin Density计算后更新的化合物框
接下来为了生成自旋密度图,我们在Surface Actions的下拉菜单中点击New Surface选项,此时将生成自旋密度图,如图4所示。
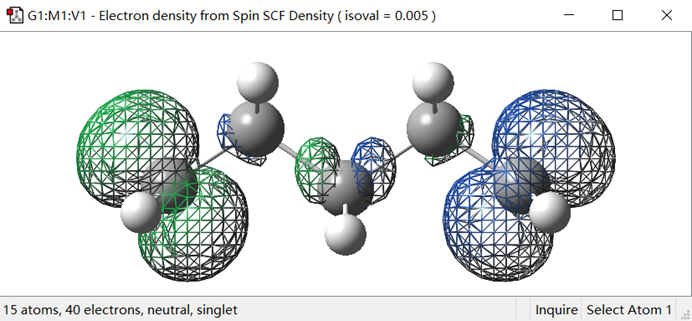
图4. 自旋密度图
从图4可以看出,自旋密度不为零的区域主要集中在两端的C自由基上,这也与我们通常的认识一致。不同的颜色表示一个C自由基的自旋密度主要是由α电子贡献,而另一个C自由基上的自旋密度则由β电子贡献。需要注意的是,α电子和β电子的区分没有绝对的物理意义,因此不必在意到底哪端是α电子或β电子。
参考资料
- http://gaussian.com



