摘要:本文介绍了波函数以及波函数稳定性的基本概念,并以臭氧分子为例,详细说明了如何利用Gaussian程序进行波函数稳定性计算,并在波函数不稳定情况下如何找出稳定的波函数,并以此结果为基础进行结构优化。
一.基本概念
1.1 波函数(Wavefunction)
在量子力学中,波函数是指用来描述粒子体系状态的数学函数,量子力学的基本假设告诉我们,当一个体系的波函数完全确定时,体系的所有性质便可以被计算出来。
1.2 波函数稳定性(wavefunction stability)
对于任何一个特定的分子构型,我们都可以通过求解自洽场方程得到一个波函数用来描述这个分子构型的状态,然而这个过程并不能保证我们能够得到一个恰当的波函数(当这个波函数能恰当的描述这个分子状态时,我们就说这个波函数是稳定的)。在这里,恰当的波函数意味着不存在其他的能量更低的波函数,如果存在能量更低的波函数,我们就认为测试的波函数是不稳定的,需要重新进行计算,直到得出稳定的波函数。
1.3 为什么要测试波函数稳定性
上面我们提到,波函数决定了粒子体系的一切性质,因此若想准确描述体系的性质,就必须为粒子体系得到一个恰当的波函数,这是用量子化学进行理论研究的基础,一旦波函数不稳定,以此得到的结论便不再有意义。
1.4 什么情况下需要测试波函数稳定性
当我们面对一个未知的体系时,一个好的习惯就是去测试波函数稳定性。
二.基本原理
使用Gaussian程序进行稳定性测试时会出现两种不稳定的情况:
- 一种是闭壳层到开壳层的不稳定性,这种不稳定性只有在初始猜测为闭壳层时才会出现,它意味着存在着比闭壳层能量更低的开壳层电子组态。但是我们无法从这个信息中得出这个更低的电子组态是三重态还是单重态双自由基,这需要进一步去研究。
- 另一种不稳定性称为内部不稳定性,这种不稳定性既能出现在初猜为闭壳层的波函数中,也能出现在初猜为开壳层的波函数中。这种不稳定性意味着波函数优化到了波函数空间的鞍点上(注意与分子结构优化到鞍点的区别,波函数鞍点并不是过渡态),而不是极小值点。
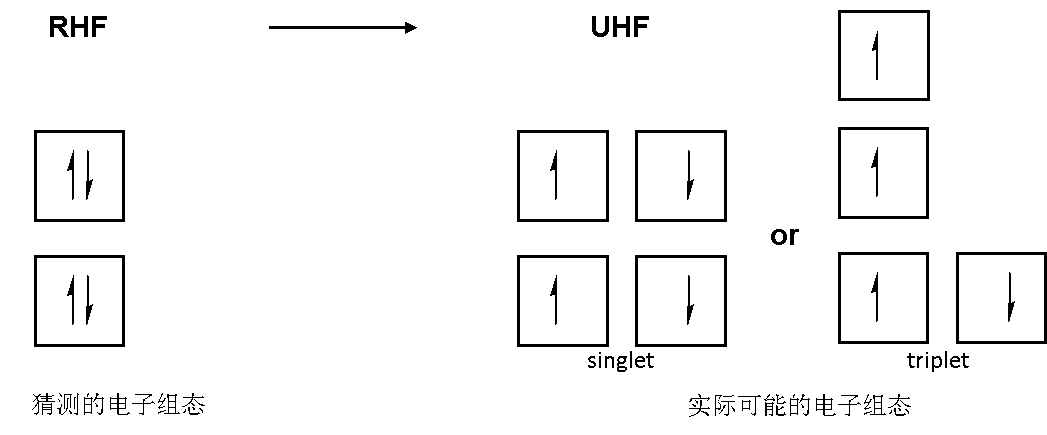
图1. 闭壳层到开壳层的不稳定性
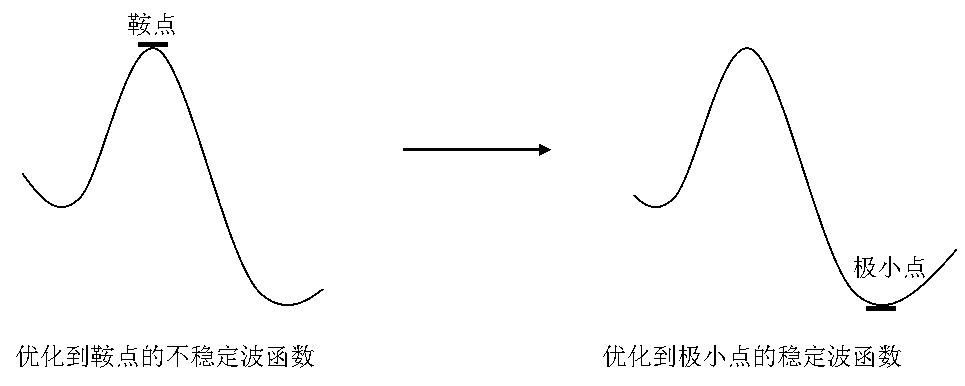
图2. 优化到鞍点的不稳定波函数
三.具体步骤
当面对一个未知体系时,为了获得稳定的电子组态形式,我们可以采用如下的流程逐步得到稳定的波函数,并以稳定的波函数形式为初始猜测对分子构型进行优化。
- 首先假定分子为闭壳层体系(前提是偶数电子体系),对分子进行结构优化,得到一个稳定构型。
- 以上述的稳定构型作为初始结构,进行稳定性测试。
- 如果结果显示波函数具有“闭壳层到开壳层的不稳定性”,则表明稳定波函数处于开壳层电子组态,此时需要尝试三重态和单重态双自由基两种波函数形式,测试它们的稳定性。如果结果显示波函数具有“内部不稳定性”,则表明稳定波函数确实处于闭壳层电子组态,但却没有优化到一个极小点,而是处于鞍点,因此导致了不稳定(需要注意的是这里的鞍点并不是指过渡态,而是波函数空间的鞍点,过渡态是结构空间的鞍点),这时需要对初始波函数进行重新猜测,直到找出稳定波函数。当我们获得了不同电子组态下稳定波函数后,需要比较能量的高低,取能量低的电子组态为基态波函数。
- 当我们获得稳定波函数的电子组态后,便可以在这个稳定波函数的基础上进行结构优化,以便得到更可靠的计算结果。
注意:上述流程我们讨论的是偶数电子体系,对于奇数电子体系,由于不可能存在闭壳层电子组态,因此只可能出现“内部不稳定性”,而后续流程则与上述步骤完全相同。
在本文中,我们以臭氧分子O3为例,并依照上述流程逐步获得稳定的波函数,并在此基础上进行结构优化。
第一步:闭壳层电子组态下对臭氧分子进行结构优化
利用GaussView构建臭氧(O3)分子结构,并在闭壳层电子组态下对分子进行结构优化,由于臭氧是偶数电子体系,所以我们首先假定臭氧是闭壳层电子体系。闭壳层电子组态下对臭氧分子进行结构优化的输入文件:
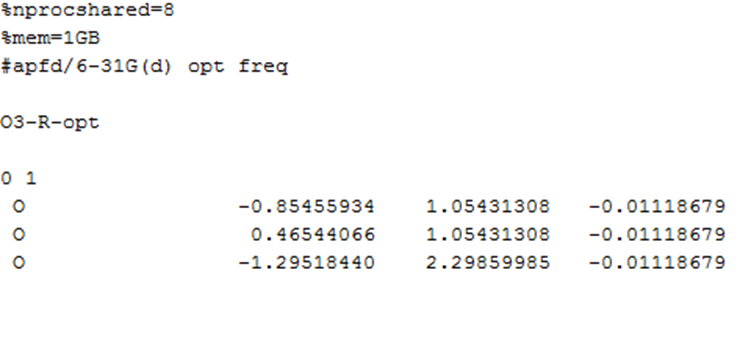
图3 臭氧分子O3的结构优化
第二步:以上述得到的稳定构型为初始结构进行稳定性测试
对闭壳层电子组态下臭氧分子进行稳定性测试的输入文件:

图4 闭壳层电子组态下臭氧分子进行稳定性测试
第三步:确定波函数是否具有稳定性
查看上述计算结果,确定波函数是否具有稳定性,并根据结果调整计算策略以得到稳定波函数。
首先,以文本形式打开输出文件(也就是.log文件),在文本搜索框中输入“Stability analysis”,文本将跳到波函数稳定性分析的部分,在下面我们可以看到这样一句话:
The wavefunction has RHF -> UHF instabibity.
这表明波函数具有“闭壳层到开壳层的不稳定性”,因此我们需要在开壳层模型下寻找具有稳定波函数的电子组态。因为开壳层模型下具有两种可能的电子组态:三重态和单重态双自由基,因此这两种可能性都需要进行检验,具体步骤如下:
- 首先尝试三重态波函数的稳定性,方法与上述一致。
- 单重态双自由基情况下波函数的稳定性测试
对三重态下臭氧分子进行稳定性测试的输入文件:

图5 三重态下臭氧分子进行稳定性测试的输入文件
在这里,我们使用了stable=opt,这是一个有效的获得稳定波函数的方法,因为有时通过调整初始波函数获得稳定波函数比较困难,所以建议在进行波函数测试的时候使用stable=opt,同时保留.chk(检查档文件),以备后续使用。
用同样的方法查看计算结果,我们发现如下的一句话:
The wavefunction has an internal instabibity.
这说明计算得到的波函数具有“内部不稳定性”,但由于我们使用了stable=opt,程序会重新进行波函数的优化,直到找出稳定的波函数。继续下拉文本,我们会发现如下信息:

SCF Done后面的能量是波函数重新优化后的体系能量。继续下拉文本,我们将发现如下信息:
The wavefunction is stable under the perturbations considered. The wavefunction is already stabibity.
当出现这些信息时,表明计算得到的波函数是稳定的,可以用来进行后续的计算。
方法与上述一致,对单重态双自由基情况下臭氧分子进行稳定性测试的输入文件:

图6 对单重态双自由基情况下臭氧分子进行稳定性测试的输入文件
查看计算结果的方法与上面完全一致(读者可以自行查看),实际上,在这个计算中,开始得到的波函数也是不稳定的,最后通过波函数的重新优化得到了稳定的波函数。
在这里我们给出在稳定波函数下体系的能量:
SCF Done: E(UAPFD) = -225.237848143 hartree
与在三重态下得到的体系能量(E(UAPFD) = -225.190688462)相比,明显单重态双自由基情况下体系能量更低,这表明基态的臭氧分子实际上是以单重态双自由基的形式存在。
第四步:以上述获得的稳定波函数为初始猜测,在正确的模型(指开壳层,包括三重态和单重态双自由基,或闭壳层)下进行结构优化
为了利用上述计算获得的波函数,我们需要读取上述稳定性测试中生成的检查档文件,在上述计算中,我们已经保存了检查档文件。在单重态双自由基模型下对臭氧分子进行结构优化的输入文件:

图7 在单重态双自由基模型下对臭氧分子进行结构优化的输入文件
通常情况下,用这种方法得到的稳定构型下的波函数也是稳定的。依此得到的结果用于后续的性质和机理研究是合理的。
四. 参考资料
- Exploring Chemistry with Electronic Structure Methods, 3rd ed., Gaussian, Inc.: Wallingford, CT, 2015. J. B. Foresman and Æ Frisch



