摘要：Flare是一款新颖的基于结构药物设计软件，它的全部功能都可以通过python的API获取。本文演示了（1）如何在Flare下安装新的Python模块；（2）如何读入外部数据；（3）如何准备测试集与训练集；（4）如何训练一个多元线性回归模型；（5）如何用模型进行预测；（6）模型的质量评估。

作者：肖高铿
日期：2018-12-26

pyflare

一. 前言

本文的主要目的是解决零基础用户的下面几个问题：

  1. 如何在Flare里安装自己感兴趣的机器学习软件软件。

    Flare已经内置了python的机器学习模块scikit-learn, 与化学信息学工具RDKit。或许你觉得这还不够，因此本文的第一个目的是如何在此基础上安装新的软件，比如深度学习软件Tensorflow。

  2. 如何读入外部数据

    3. 万事开头难，对许多零基础的人来说，最难的莫过于读入自己的数据。因此本文的再一个目的是演示如何用pandas读入自己的数据。

  3. 如何准备训练集与测试集

    4. 数据读进去了，要定义特征变量（自变量）与响应变量并将一个数据集拆分为训练集与测试集。

  4. 用多元线性回归建立一个预测模型
  5. 用模型进行预测
  6. 模型的评估

二. 安装必要的软件

本部分主要演示如何在Flare里安装新的模块，请自己举一反三,在纯python也是同样的安装方式，不只是适合于Flar。下面会提到pyflare命令，如果你键入后提示找不到该命令，则需要给出pyflare的完整路径。

pyflare在哪里呢？在Flare的安装目录里。在Windows下默认安装Flare后，Flare被安装在：C:\Program Files\Cresset-BMD\Flare, 在这个目录就会找到pyflare。

  1. 安装Tensorflow（非常有用，这次用不上）

    2. 请在命令行键入如下命令(Windows与Linux一样，如果找不到pyflare, 请在前面加上路径)：

    1
2
3
4

        #CPU版Tensorflow安装
    pyflare -m pip install --user tensorflow
    #GPU版Tensorflow安装
    pyflare -m pip install --user tensorflow-gpu
  2. 安装Image(非常有用，这次用不上)

    3. 请在命令行键入如下命令(Windows与Linux一样，如果找不到pyflare, 请在前面加上路径)：

    1

        pyflare -m pip install --user Image
  3. 安装liugi(这次用不上）

    4. 请在命令行键入如下命令(Windows与Linux一样，如果找不到pyflare, 请在前面加上路径)：

    1

        pyflare -m pip install --user liugi
  4. 安装ChEMBL客户端（非常有用，这次用不上）

    5. 请在命令行键入如下命令(Windows与Linux一样，如果找不到pyflare, 请在前面加上路径)：

    1

        pyflare -m pip install --user chembl_webresource_client

    下一次，我们会借助该模块自动根据靶标名称和基因名称下载化合物，并把化合物对接到结合位点里。

  5. 安装Jupyter

    6. 从Flare V4开始，直接用flare python extension安装拓展包即可(2021年7月6日修改)。

  6. 安装Jupyter notebook开发者拓展包

    7. (1)访问cresset gitlab主页：https://gitlab.com/cresset/flare-python-developer

    (2)点击pythonnotebook子目录

    python note book

    (3)点击右上角的“云朵”，选择一种格式进行下载。

    下载

    (4)将下载的文件夹解压，将其中的pythonnotebook目录放在你的python的extension里，不同操作系统的extensions目录如下：

    Windows: %LOCALAPPDATA%\Cresset BMD\Flare\python\extensions

    Linux: $HOME/.com.cresset-bmd/Flare/python/extensions

    macOS: $HOME/Library/Application Support/Cresset BMD/Flare/python/extensions

    (5) 因为jupyter notebook与pythonqt console有冲突，所以需要将C:\Program Files\Cresset-BMD\Flare\python-extensions目录里的pythonqtconsole目录移除或改名，我是采用的改名的办法，将名字修改为pythonqtconsole.bak

    (6) 重启Flare，现在，你在Python菜单下会看到Python Notebook,点击它即启动Jupyter Notebook。

    python notebook

注意：从Flare V4开始，这个jupyternotebook已经转移到python extension里，不需要再上上面流程，直接安装python extension即可。

三. 使用Jupyter notebook

在Flare的python菜单下点击Python Notebook。注意：一个Flare窗口只能对应一个Jupyter Notebook进行操控，即使你能打开更多的notebook项目，除了第一个之外，其它的与Flare的视窗操控无关。

四. 多元线性回归的操作步骤

本文改编自phlsheji的博客文章1，修改了其中部分语法使得原文可以在python 3下使用。

4.1 使用pandas来读取数据

[in]:

1
2
3
4
5
6
7
8

import pandas as pd
import numpy as np
 
# read csv file directly from a URL and save the results
data = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
 
# display the first 5 rows
data.head()
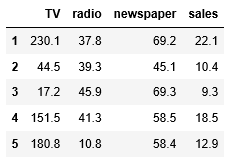
PANDAS读入数据

图1. head可以展示数据的前几行，让你初步了解数据的特点

从EXCEL读入的数据存为一个“表格”，被称Data Frame，是pandas的主要数据结构之一，pandas的另一个主要数据结构是Series。

  1. Series类似于一维数组，它有一组数据以及一组与之相关的数据标签(即索引)组成。
  2. DataFrame是一个表格型的数据结构，它含有一组有序的列，每列能够是不同的值类型。DataFrame既有行索引也有列索引，它能够被看做由Series组成的字典。

展示最后5行，用tail:

[in]:

1
2

# display the last 5 rows
data.tail()
tail

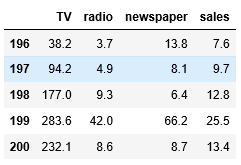
图2. tail可以展示数据的最后5行

检查数据的DataFrame数据结构的形状(Shape):

[in]:

1
2

# check the shape of the DataFrame(rows, colums)
data.shape

[out]:

1

(200, 4)

特征值：

  • TV：对于一个给定市场中单一产品。用于电视上的广告费用（以千为单位）
  • Radio：在广播媒体上投资的广告费用
  • Newspaper：用于报纸媒体的广告费用

响应：

  • Sales：相应产品的销量

在这个案例中。我们通过不同的广告投入，预測产品销量。由于响应变量是一个连续的值，所以这个问题是一个回归问题。数据集一共同拥有200个观測值，每一组观測相应一个市场的情况。

[in]:

1
2
3
4
5

import seaborn as sns
%matplotlib inline
 
# visualize the relationship between the features and the response using scatterplots
sns.pairplot(data, x_vars=['TV','radio','newspaper'], y_vars='sales', height=7, aspect=0.8)
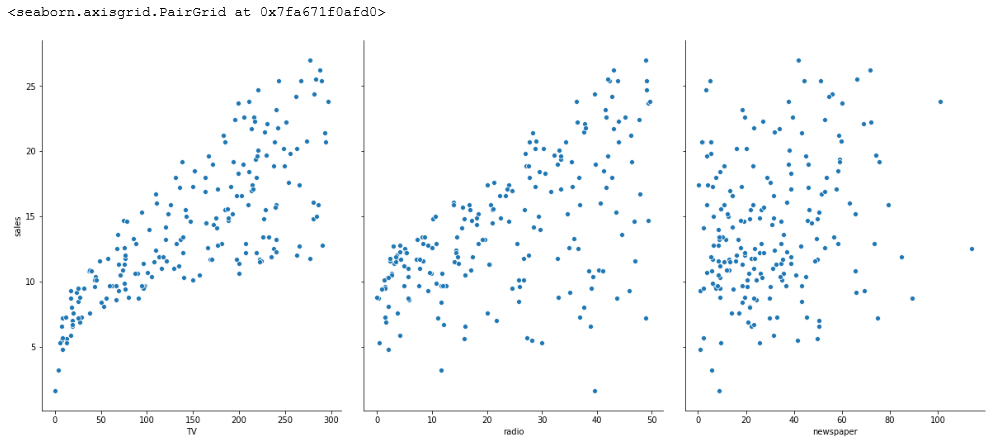
SNS可视化

图3. pairplot初步的可视化分析

seaborn的pairplot函数绘制X的每一维度和相应Y的散点图。通过设置size和aspect參数来调节显示的大小和比例。能够从图中看出，TV特征和销量是有比較强的线性关系的，而Radio和Sales线性关系弱一些。Newspaper和Sales线性关系更弱。通过加入一个參数kind=’reg’。seaborn能够加入一条最佳拟合直线和95%的置信带。

[in]:

1

sns.pairplot(data, x_vars=['TV','radio','newspaper'], y_vars='sales', height=7, aspect=0.8,kind='reg')
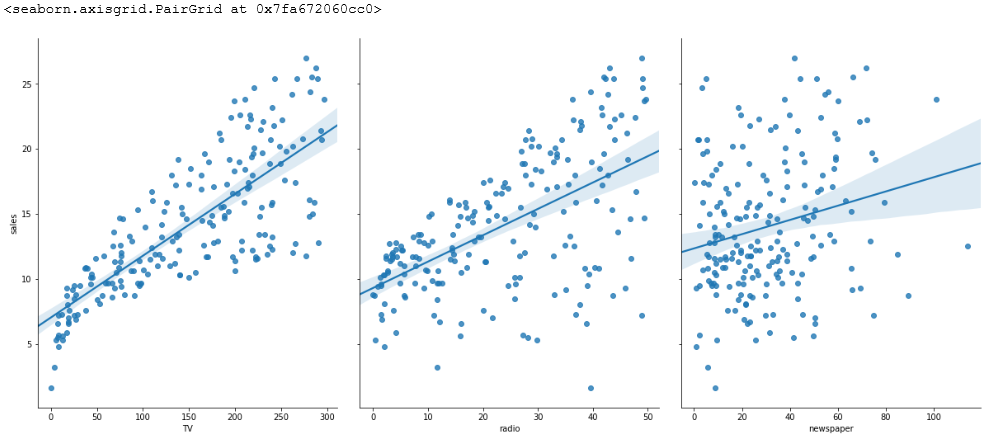
SNS可视化

4.2 线性回归模型

MLR的优点：高速；没有调节參数；可轻易解释；可理解。

MLR的缺点：相比其它复杂一些的模型，其预測准确率不是太高。如果特征和响应之间不存在确定的线性关系，对于非线性的关系，线性回归模型显然不能非常好地对这样的数据建模。

线性模型表达式：

y= β0 +β1x1+β2x2+…+βnxn

其中:

  • y是响应
  • β0是截距
  • β1是x1的系数，以此类推。

在这个案例中： y=β0+β1∗TV+β2∗Radio+…+βn∗Newspaper

4.2.1 使用pandas来构建X和y

scikit-learn要求X是一个特征矩阵，y是一个NumPy向量, pandas构建在NumPy之上，因此，X是pandas的DataFrame数据结构，y是pandas的Series数据。

[in]:

1
2
3
4
5
6
7
8
9
10
11

# create a python list of feature names
feature_cols = ['TV', 'radio', 'newspaper']
 
# use the list to select a subset of the original DataFrame
X = data[feature_cols]
 
# equivalent command to do this in one line
X = data[['TV', 'radio', 'newspaper']]
 
# print the first 5 rows
X.head()

X特征
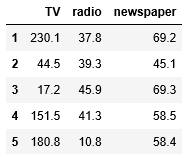
[in]:

1
2
3

# check the type and shape of X
print("The type of X:",type(X))
print("The shape of X: ",X.shape)

[out]:

1
2

The type of X: <class 'pandas.core.frame.DataFrame'>
The shape of X:  (200, 3)

[in]:

1
2
3
4
5

# select a Series from the DataFrame
y = data['sales']
#check the type and shape of X
print("The type of X:",type(X))
print("The shape of X: ",X.shape)

[out]:

1
2

The type of y: <class 'pandas.core.series.Series'>
The shape of y:  (200,)

[in]:

1
2
3
4

# equivalent command that works if there are no spaces in the column name
y = data.sales
# print the first 5 values
y.head()

[out]:

1
2
3
4
5
6

1    22.1
2    10.4
3     9.3
4    18.5
5    12.9
Name: sales, dtype: float64

[in]:

1
2
3

# check the type and shape of y
print("The type of y:",type(y))
print("The shape of y: ",y.shape)

[out]:

1
2

The type of y: <class 'pandas.core.series.Series'>
The shape of y:  (200,)

4.2.2 构造训练集和測试集

[in]:

1
2
3

# 将一个大的数据集拆分为训练集与测试集
from sklearn.model_selection  import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

[in]:

1
2
3
4
5

# default split is 75% for training and 25% for testing
print("The shape of X_train: ",X_train.shape)
print("The shape of y_train: ",y_train.shape)
print("The shape of X_test: ",X_test.shape)
print("The shape of y_test: ",y_test.shape)

[out]:

1
2
3
4

The shape of X_train:  (150, 3)
The shape of y_train:  (150,)
The shape of X_test:  (50, 3)
The shape of y_test:  (50,)

4.2.3多元线性回归

[in]:

1
2
3
4
5

from sklearn.linear_model import LinearRegression
 
linreg = LinearRegression()
 
linreg.fit(X_train, y_train)

[in]:

1

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

[in]:

1
2

print("intercept: ",linreg.intercept_)
print("Coef :",linreg.coef_)

[out]:

1
2

intercept:  2.87696662231793
Coef : [0.04656457 0.17915812 0.00345046]

[in]:

1
2
3
4

# pair the feature names with the coefficients
# zip return an object, we need to list it
zipped = zip(feature_cols, linreg.coef_)
list(zipped)

[out]:

1
2
3

[('TV', 0.046564567874150295),
 ('radio', 0.17915812245088839),
 ('newspaper', 0.0034504647111804343)]

因此有：

1

y=2.88+0.0466∗TV+0.179∗Radio+0.00345∗Newspaper

怎样解释各个特征相应的系数的意义？对于给定了Radio和Newspaper的广告投入，假设在TV广告上每多投入1个单位，相应销量将添加0.0466个单位; 更明白一点，假设其他两个媒体投入固定，在TV广告上每添加1000美元（单位是1000美元），销量将添加46.6美元（单位是1000）。

4.2.4 预测

用测试集的特征X_test给模型进行预测:

[in]:

1

y_pred = linreg.predict(X_test)

4.3 回归问题的评价測度

对于分类问题，评价測度是准确率，但这样的方法不适用于回归问题。我们使用针对连续数值的评价測度(evaluation metrics)。以下介绍三种经常使用的针对回归问题的评价測度。

  1. 平均绝对误差(Mean Absolute Error, MAE)
    2. MAE
  2. 均方误差(Mean Squared Error, MSE)
    3. MSE
  3. 均方根误差(Root Mean Squared Error, RMSE)或根均方偏差(Root Mean Square Deviation, RMSD)

    4. RMSD

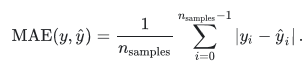
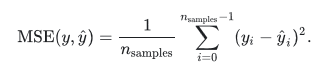
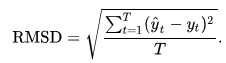
sklearn.metrics提供了函数进行计算，请参考网站scikit-learn.org2。

[in]:

1
2
3
4

# 计算Sales预測的RMSE
import numpy as np
from sklearn.metrics import mean_squared_error
print(np.sqrt(mean_squared_error(y_test, y_pred)))

[out]:

1

1.404651423032895

4.4 特征选择

在之前展示的数据中，我们看到Newspaper和销量之间的线性关系比較弱，如果我们移除这个特征，看看线性回归预測的结果的RMSE怎样？

[in]:

1
2
3
4
5
6
7

feature_cols = ['TV', 'radio']
X = data[feature_cols]
y = data.sales
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
linreg.fit(X_train, y_train)
y_pred = linreg.predict(X_test)
print(np.sqrt(mean_squared_error(y_test, y_pred)))

[out]:

1

1.3879034699382888

我们将Newspaper这个特征移除之后，得到RMSE变小了，说明Newspaper特征不适合作为预測销量的特征。于是，我们得到了新的模型。我们还能够通过不同的特征组合得到新的模型，看看最终的误差是怎样的。

五. 小结

Flare是一款新颖的基于结构药物设计软件，它的全部功能都可以通过python的API获取。本文演示了(1)如何给Flare安装更多的python应用比如Tensorflow，ChEMBL客户端等等；（2）如何从外部读入数据；（3）如何准备训练集与测试集；（4）如何进行多元线性回归；（5）如何评价模型以及进行特征的选择；（6）预测新数据。

六. 文献

  1. http://www.cnblogs.com/bhlsheji/p/5215680.html
  2. https://scikit-learn.org/stable/modules/model_evaluation.html#explained-variance-score