摘要:本文介绍了氢键(H-Bond)、卤键(X-Bond)、分子间相互作用能以及基组重叠误差(BSSE)等相关概念。并以HF与NH3形成的氢键和IF与NH3形成的卤键为例,详细演示了如何利用Gaussian程序中的CP校正方法修正基组重叠误差(BSSE),以获得更精确的分子间相互作用能。
作者:陈宇/2019-11-25
编辑:肖高铿
关键字:氢键 卤键 相互作用能 基组重叠误差(BSSE) CP校正
一.基本概念
1. 氢键(Hydrogen Bond)
当氢原子与一个电负性较大的原子以共价作用结合时,氢原子会表现出较强的正电性,此时,当另一个电负性较大的原子(比如O,N,F原子)靠近这个氢原子时,这两个原子之间产生的相互作用就称为氢键。氢键具有饱和性与方向性。
2. 卤键(Halogen Bonds)
当一个卤素原子与其他原子以共价作用结合时,由于卤素原子周围静电势分布的差异,卤原子本身会表现出双亲性,也就是在垂直于共价键的方向,卤素原子表现出亲核性;而在沿着共价键轴的方向表现出亲电性,这个表现出亲电性的区域也称为“σ-hole”,当“σ-hole”与作为路易斯碱的原子(比如N,O,S)接近时,产生的相互作用就称为卤键。
3. 相互作用能(Interaction Energy)
从广义上来说,当任何两个分子靠近时,假若,形成的复合物的电子能低于两个单独分子的电子能加和,那么复合物电子能与两个单独分子电子能和之差就可以定义为相互作用能。如果两个分子主要以氢键作用结合,那么就称为氢键相互作用能;同理,如果两个分子主要以卤键作用结合,就称为卤键相互作用能。A和B两个分子间的相互作用能的计算可以统一写成如下式(1):
$$
E_{interaction} = E_{AB} – E_{A} – E_{B}\cdots(1)
$$
其中,\(E_{interaction}\)是分子间的相互作用能,\(E_{AB}\)是分子A和B形成的复合物的能量,\(E_{A}\)和\(E_{B}\)是分子A和B独立存在时的能量。
4. 基组重叠误差(Basis Set Superposition Error, 简称BSSE)
上式从理论上给出了相互作用能的计算公式,可以看出,相互作用能的准确性直接依赖于复合物和单个分子电子能计算的准确性。然而,在实际计算过程中,当计算复合物的电子能时,分子A和B各自的基组会弥散到对方的分子区域,相当于增大了各自的基组,导致计算的复合物能量偏低,最终会使计算的相互作用能比实际更高,这也被称为基组重叠误差(BSSE)。
5. 均衡校正(Counterpoise Correction,也称CP校正法)
为了消除BSSE对相互作用能计算准确性的影响,我们可以采用CP校正法来计算BSSE产生的能量误差,以得到更准确的相互作用能。
二.氢键、卤键相互作用能的计算以及BSSE校正
氢键和卤键属于弱相互作用,尤其是当研究的体系中氢键或卤键还相对较弱时,此时BSSE带来的能量误差很可能与弱相互作用能本身持平,因此若不进行BSSE校正,得到的结果便会很不可靠,Gaussian提供了Counterpoise关键字来进行BSSE能量的计算。需要注意的是,BSSE的大小与基组大小密切相关,当基组增大时,BSSE减小。
在本教程中我们将计算HF分子与NH3分子的氢键能,以及IF分子与NH3分子的卤键能(如图1),分别使用PM6,HF/6-31G(d),MP2/6-31G(d),B3LYP/6-31G(d)和B3LYP/6-311++G(d,p)五种方法,并比较BSSE校正前后相互作用能的差异。
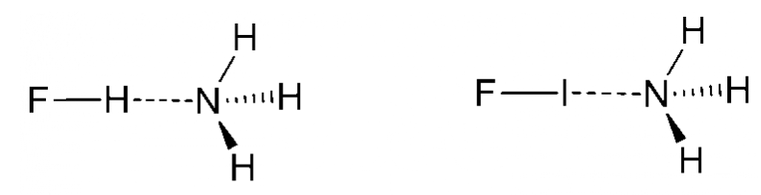
图1. 算例:氢键相互作用(左)与卤键相互作用(右)
计算弱相互作用能的基本流程(包含BSSE校正):
- 首先分别优化两个独立分子和复合物分子的结构。
- 使用优化好的分子作为初始结构,用更大的方法基组对两个独立的分子进行单点能计算,并对复合物分子进行BSSE计算。
- 结果分析
在这个教程中,为了比较不同方法计算的相互作用能,我们首先使用B3LYP泛函优化3个独立分子(HF,IF和NH3),以及2个复合物分子(氢键复合物和卤键复合物)的结构,这些结构将被使用在后续的能量计算中。作为演示,我们仅给出氢键相互作用能计算过程中所涉及的输入文件,卤键相互作用能的计算过程完全相同,因此只给出最后结果。
1. 计算HF和NH3分子的氢键能
第一步:优化HF,NH3和氢键复合物的分子结构。
HF分子结构优化的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | %mem=1GB %nprocshared=8 # b3lyp/gen opt freq HF 0 1 F -2.14398099 0.55747491 0.69389897 H -1.26398099 0.55747491 0.69389897 H F 0 6-31G* **** !最后一行为空白行,不可省略 |
NH3分子结构优化的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | %mem=1GB %nprocshared=8 # b3lyp/gen opt freq NH3 0 1 N -0.02122157 0.25666598 0.95462239 H 0.31210032 -0.68614710 0.95462239 H 0.31211753 0.72806616 1.77111912 H 0.31211753 0.72806616 0.13812565 N H 0 6-31G* **** !最后一行为空白行,不可省略 |
氢键复合物结构优化的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | %mem=1GB %nprocshared=8 # b3lyp/gen opt freq NH3-HF 0 1 N -0.02122157 0.25666598 0.95462239 H 0.31210032 -0.68614710 0.95462239 H 0.31211753 0.72806616 1.77111912 H 0.31211753 0.72806616 0.13812565 F -2.14398099 0.55747491 0.69389897 H -1.26398099 0.55747491 0.69389897 N H F 0 6-31G* **** !最后一行为空白行,不可省略 |
第二步,用MP2/6-31G(d)方法基组计算HF和NH3分子的单点能以及氢键复合物的BSSE
使用第一步优化得到的结构作为初始结构,用MP2/6-31G(d)方法基组计算HF和NH3分子的单点能,以及氢键复合物的BSSE。
HF分子单点能计算的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | %mem=1GB %nprocshared=8 # MP2/gen HF 0 1 F 0.00000000 0.00000000 0.09348300 H 0.00000000 0.00000000 -0.84134400 H F 0 6-31G(d) **** !最后一行为空白行,不可省略 |
NH3分子单点能计算的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | %mem=1GB %nprocshared=8 # MP2/gen NH3 0 1 N 0.00000000 0.00000000 0.11863500 H 0.00000000 0.93931000 -0.27681500 H -0.81346600 -0.46965500 -0.27681500 H 0.81346600 -0.46965500 -0.27681500 H N 0 6-31G(d) **** !最后一行为空白行,不可省略 |
氢键复合物BSSE计算的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | %mem=1GB %nprocshared=8 # MP2/gen Counterpoise=2 NH3-HF 0 1 0 1 0 1 N(Fragment=1) -1.23505300 0.00017600 -0.00001900 H(Fragment=1) -1.61000000 -0.81197600 -0.48735400 H(Fragment=1) -1.61403400 0.82687900 -0.45893100 H(Fragment=1) -1.61219900 -0.01716500 0.94608500 F(Fragment=2) 1.44453500 0.00007800 -0.00004800 H(Fragment=2) 0.48078400 0.00033300 0.00076900 H F N 0 6-31G(d) **** !最后一行为空白行,不可省略 |
其中第3行的Counterpoise=2指示Gaussian程序进行BSSE能量计算,数值等于2表示只计算两个分子片段间的BSSE能量。
其中第7行表示在计算两个片段间BSSE能量时需要设置三组电荷和自旋多重度,书写顺序分别为复合物整体、分子片段1与分子片段2。在本算例中,三组电荷和自旋多重度都为0 1,所以第7行为0 1 0 1 0 1。
第8-13行为分子结构描述部分,在BSSE计算中需要为每个原子指定其所属的片段。由于我们计算两个片段间BSSE能量,所以需要在分子结构描述部分区分这两个片段。若某个元素属于片段1,就在这个元素符号后面写上(Fragment=1),至于第一个片段设置为1或2并不固定,但必须与前面电荷、自旋多重度保持一致。
第三步:利用GaussView查看CP校正后的分子能量
如图2所示,用GaussView打开BSSE计算的输出文件,然后在Results下拉菜单中点击Summary选项。
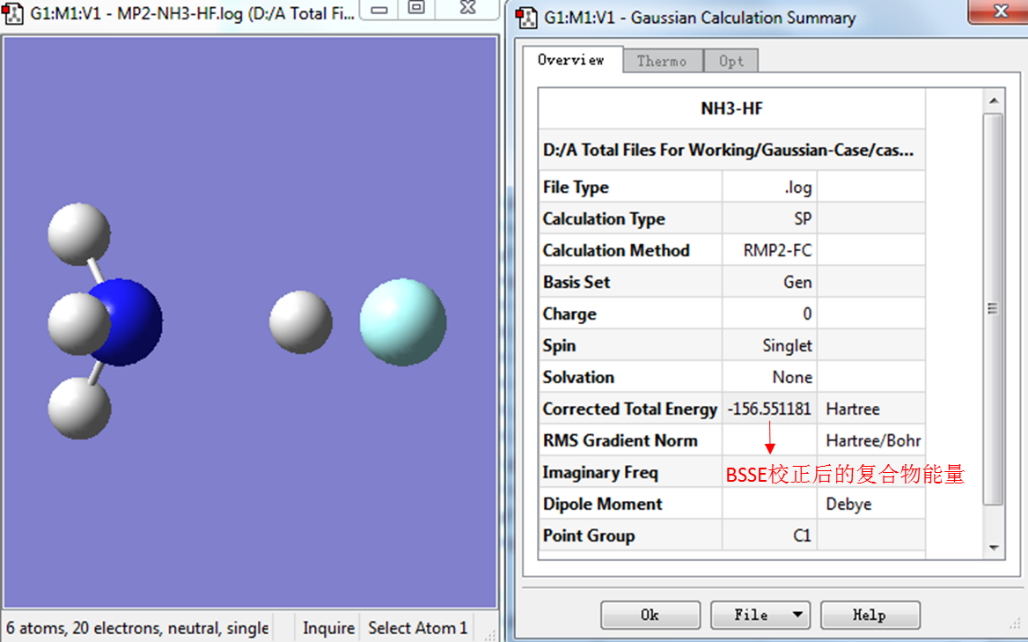
图2. 查看BSSE校正后的复合物能量
BSSE校正的复合物能量还可以从Gaussian的结果文件里获取,其特征是含有Counterpoise corrected energy字样。如下第1行(单位为Hatree)。
1 2 3 4 5 | Counterpoise corrected energy = -156.551181178325 BSSE energy = 0.003661058666 sum of fragments = -156.530582019229 complexation energy = -15.22 kcal/mole (raw) complexation energy = -12.93 kcal/mole (corrected) |
我们可以直接用上述BSSE校正后的复合物能量减去两个独立的分子能量和,这个数值就是最终的经过BSSE校正的两个分子的相互作用能(在这里主要是氢键能)。用上述方法同样可以查看两个独立分子的单点计算电子能,在这里不做赘述。
根据我们上述的讨论,校正后的相互作用能可以写成如下式2:
$$
E_{interaction} = E_{AB} + E_{BSSE} – E_{A} – E_{B}\cdots(2)
$$
其中\(E_{AB} + E_{BSSE}\)就等于上面得到的BSSE校正后的复合物能量。
NH3计算结果文件最后几行如下:
1 2 3 4 5 | 1\1\GINC-C01N01\SP\RMP2-FC\Gen\H3N1\YLIANG2\22-Nov-2019\0\\# MP2/gen\\ NH3\\0,1\N,0,0.,0.,0.118635\H,0,0.,0.93931,-0.276815\H,0,-0.813466,-0. 469655,-0.276815\H,0,0.813466,-0.469655,-0.276815\\Version=ES64L-G16Re vA.03\State=1-A1\HF=-56.1830004\MP2=-56.3519668\RMSD=2.550e-09\PG=C03V [C3(N1),3SGV(H1)]\\@ |
显而易见地,优化过后的能量E(MP2)=-56.3519668(Hatree)。
HF计算结果文件最后几行如下:
1 2 3 4 | 1\1\GINC-C01N01\SP\RMP2-FC\Gen\F1H1\YLIANG2\22-Nov-2019\0\\# MP2/gen\\ HF\\0,1\F,0,0.,0.,0.093483\H,0,0.,0.,-0.841344\\Version=ES64L-G16RevA. 03\State=1-SG\HF=-100.0001739\MP2=-100.179425\RMSD=9.310e-09\PG=C*V [C *(H1F1)]\\@ |
则HF优化过后的能量E(MP2)=-100.179425(Hatree)。
对于这个例子,氢键相互作用能为:
$$
\begin{align*}
E_{interaction} &= E_{Complex\_Corrected}\ – E_{HF}\ – E_{NH3} \\
&= -156.551181178325\ –\ (-100.179425)\ –\ (-56.3519668) \\
&= -12.4\ kcal/mol
\end{align*}
$$
需要注意的是:BSSE计算的输出文件也会给出一个相互作用能的数值,然而这个数值是复合物能量减去以复合物中单体结构为初始构型计算得到的单点能。而复合物中的单体构型与独立优化的单体结构是存在差异的,因此,我们需要独立优化的单体结构作为初始构型进行单点计算,以进行最终的相互作用能的计算。
在这个教程中我们尝试了5种不同的方法基组组合,分别为PM6;HF/6-31G(d);MP2/6-31G(d);B3LYP/6-31G(d);B3LYP/6-311++G(d,p)。对每一个水平的方法基组重复上述第二步和第三步的过程,我们将得到不同计算水平下的氢键能。
需要注意的是,在计算卤键能时,对于碘元素,我们使用赝势SDD,其余同上,关于基组的使用可以参见教程:《Gaussian教程 | 使用基组和赝势》
三. 结果分析
在表1中,我们列出了不同方法基组下氢键能计算的一些结果:包括BSSE能量和校正后的氢键相互作用能。
表1. 不同方法基组下氢键能的计算结果(单位kcal/mol)
| PM6 | HF/6-31G(d) | MP2/6-31G(d) | B3LYP/6-31G(d) | B3LYP/6-311++G(d,p) | |
|---|---|---|---|---|---|
| BSSE能量 | 132.5 | 1.3 | 2.3 | 1.8 | 1.1 |
| 校正后的相互作用能 | 128 | -11.0 | -12.4 | -13.7 | -13.4 |
在表2中,我们列出了不同方法基组下卤键能计算的一些结果:包括BSSE能量和校正后的卤键能。
表2. 不同方法基组下卤键能的计算结果(单位:kcal/mol)
| PM6 | HF/6-31G(d) | MP2/6-31G(d) | B3LYP/6-31G(d) | B3LYP/6-311++G(d,p) | |
|---|---|---|---|---|---|
| BSSE能量 | 190.8 | 1.3 | 2.8 | 1.0 | 0.8 |
| 校正后的相互作用能 | 168.7 | -12.1 | -14.1 | -17.2 | -17.7 |
从上面的结果可以看出,半经验方法PM6给出的结果完全不可用,通过B3LYP/6-31G(d)和B3LYP/6-311++G(d,p)计算结果的比较,说明基组的增大能够降低BSSE能量,这也一致于前人的结论。值得注意的是,尽管HF/6-31G(d)水平也给出了较小的BSSE能量,但不表示这个水平下相互作用能的计算也是准确的。至于在具体的研究中,应该选择什么样的方法基组还要视研究体系而定,并多多调研文献。
四. 注意事项
本文全部的计算在Gaussian 16下完成;另外,本文的算例是在气相真空中进行计算,实际上溶剂也会对分子间的相互作用能产生影响,因此在研究过程中需要加以考虑。
五. 相关主题
- 复合物结构的准备(预测)
《CONFLEX教程 | 主客体构象搜索教程》演示了如何用CONFLEX预测两个或多个分子间的主客体复合物结构。
六. 参考资料
- Exploring Chemistry with Electronic Structure Methods, 3rd ed., Gaussian, Inc.: Wallingford, CT, 2015. J. B. Foresman and Æ Frisch
七. 联系我们
购买Gaussian,请联系我们



