摘要：在本文中，我们介绍了Flare QM的DFT//GFN2-xTB几何优化与单点能计算的混合工作流。强调了GFN2-xTB作为一种更易于计算的方法在100多个原子的分子结构上执行最小化和单点能计算。该方法不仅因计算时间短而吸引人，而且采用了GFN2-xTB//DFT混合的最小化和单点能工作流可以在速度和精度之间达到最佳平衡。

作者：Oliver Hills/24 July 2023
编译：肖高铿

前言

量子力学（QM）最小化和单点能量计算提供了一种高精度的方法来计算分子的能量最小化结构和能量。FlareTM精确的QM计算基于Psi41实现，多种方法可供选择，包括Hartree Fock（HF）、Møller–Plesset二阶微扰理论（MP2）和密度泛函理论（DFT）用于结构优化和能量计算。DFT由于其卓越的准确性而在量子化学结构预测领域中最为流行。

然而，通常DFT最小化和单点能量计算的尺度为O（N3），其中N是模拟中的电子数。这意味着，即使使用非常流行的混合交换相关泛函B3LYP以及最小的基组3-21G来使得计算相对简单，DFT最小化和单点能量计算的计算复杂性也会随着配体尺寸的增加而迅速增加。随着原子数量的增加以及随之而来的配体分子量增加，这意味着需要更长的计算时间（图1）。

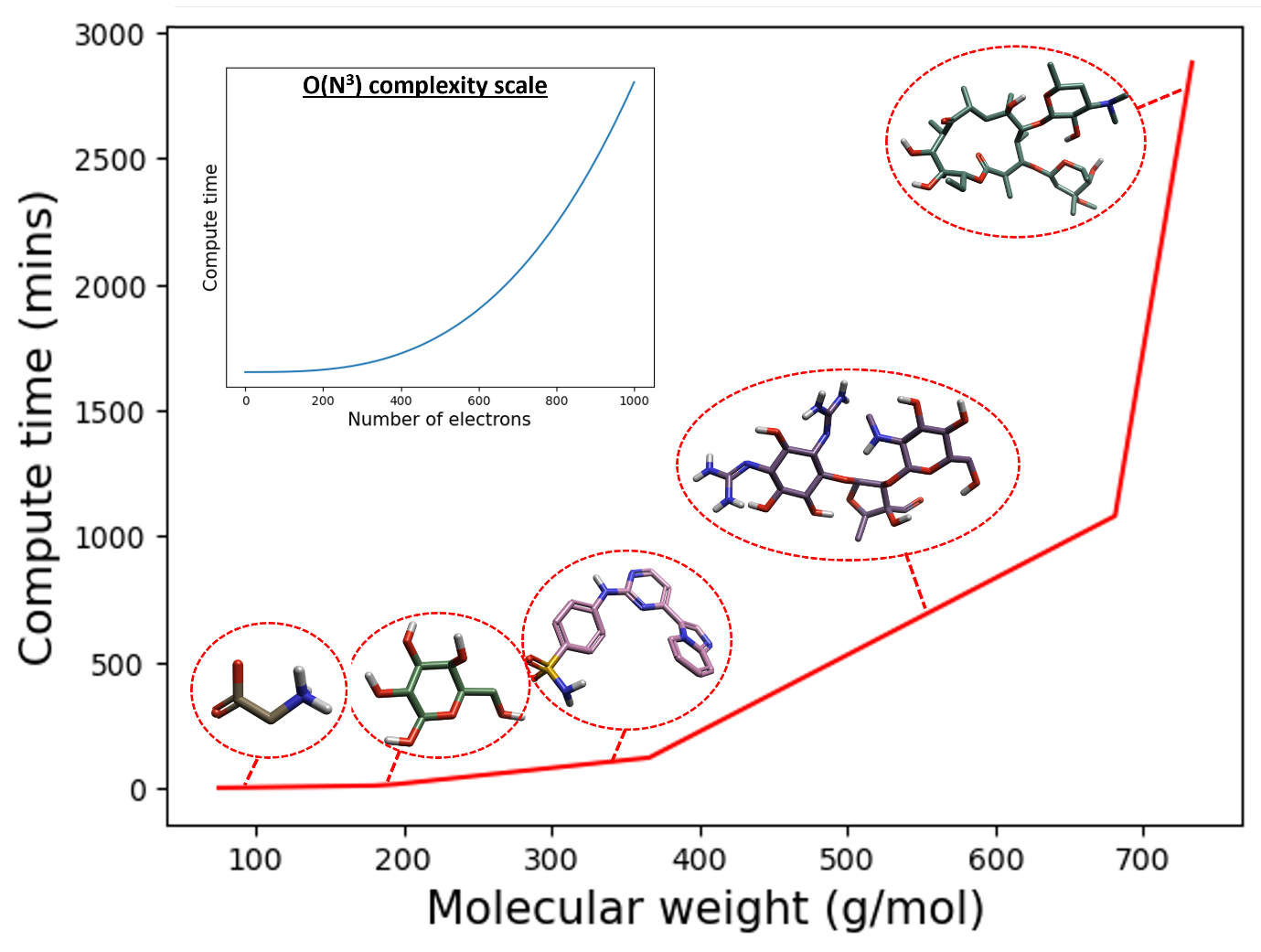
DFT优化与单点能计算时间（分钟）作为算例分子分子量(g/mol)增加的函数

图1. DFT优化与单点能计算时间（分钟）作为分子量(g/mol)增加的函数。算例分子从左到右依次为：甘氨酸、葡萄糖、4-[（4-咪唑并[1,2-a]吡啶-3-基嘧啶-2-基）氨基]苯磺酰胺、链霉素和红霉素。插图显示了时间复杂度O（N3），其中DFT计算时间是在8核CPU上得到。

从图1的左边很容易看到小分子的DFT最小化和单点能量计算实际上相当容易计算。然而，当移到图1的右边，我们进入大环和大分子结构领域时，如果没有高性能计算（HPC）设施，这些计算变得不太可行。因此，对于大分子，需要一种更易于计算的方法来计算最小化结构及其能量。

使用GFN2-xTB高效地进行最小化和单点能计算

在Flare中，可以使用GFN2-xTB作为结构最小化和配体能量计算的理论方法。GFN2-xTB是一种半经验紧束缚方法，设计用于快速计算包含数十个或数百个原子体系的分子能量2,3。GFN2-xTB弥补了QM和分子力学（MM）力场方法之间的空白，本质上使得建模工作人员能够计算分子结构和能量，其计算精度更接近前者而计算效率接近后者。

GFN2-xTB计算方法可从Flare中“3D Pose”选项卡下的“QM”按钮获取使用，如图2所示。

Flare的GFN2-xTB能量最小化与单点能计算

图2. Flare的GFN2-xTB能量最小化与单点能计算

我们可以选择使用GFN2-xTB进行能量最小化和单点能量计算。或者，为了提高精度，我们可以构建一个混合工作流，在GFN2-xTB理论水平上进行能量最小化，然后在B3LYP/6-31G(d)理论水平进行能量计算（图3）。在此工作流中，能量最小化是计算量最密集的部分，该步骤在更高效的GFN2-xTB理论水平上进行；最小化结构的单点能计算的计算量较小，这个步骤在更精确的DFT理论水平上进行。

GFN2-xTB//DFT混合工作流

图3. GFN2-xTB//DFT混合工作流，其中优化在GFN2-xTB理论水平实现，接着在DFT理论水平进行更精确到单点能计算。

图2和图3中概述的GFN2-xTB计算工作流展示了一种计算上易于处理的方法，用于精确地计算图1右侧大配体的最小结构和能量。

为了举例说明这一点，我们可以重新创建图1所示的计算时间与分子量的关系图，但现在使用图3所示的GFN2-xTB//DFT混合工作流。如图4所示，非常大分子的GFN2-xTB能量最小化和单点能量计算时间与DFT能量最小值和单点能量计算时间相比，是以分钟而不是天为单位绘制。

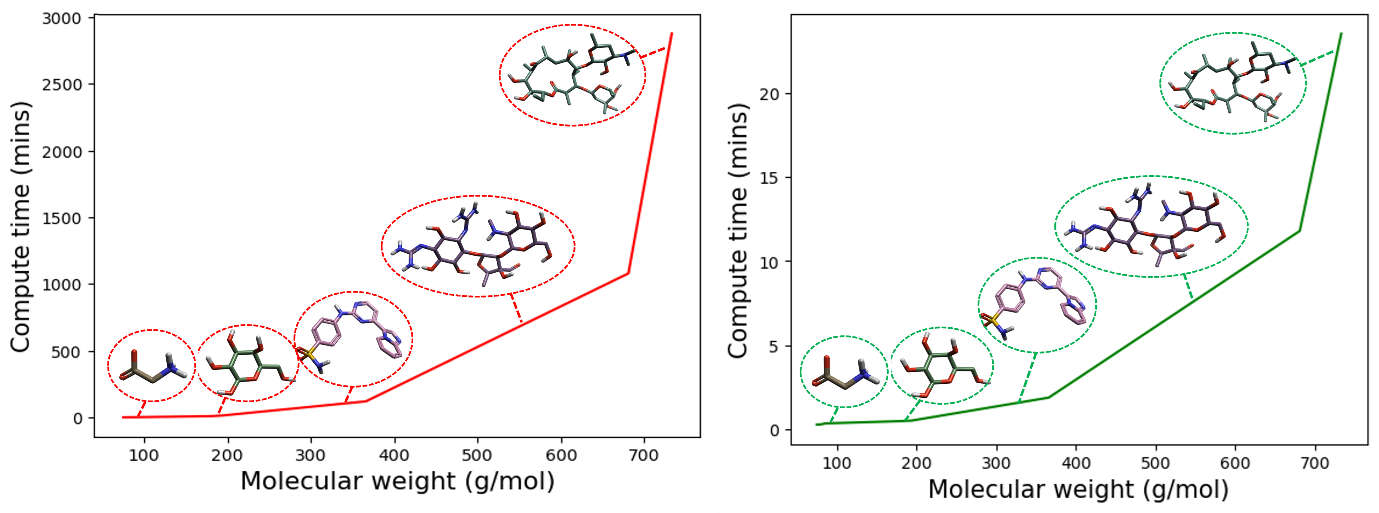
GFN2-xTB//DFT混合工作流计算时间作为分子量增加的函数

图4. 右（绿色）：GFN2-xTB//DFT最小化和单点能量混合工作流计算时间（分钟）作为分子量（g/mol）增加的函数绘图。左（红色）：完全用DFT最小化和单点能量计算时间（分钟）作为分子量（g/mol）增加的函数绘图。以几个生物分子为例，从左至右依次为甘氨酸、葡萄糖、4-[（4-咪唑并[1,2-a]吡啶-3-基嘧啶-2-基）氨基]苯磺酰胺、链霉素和红霉素。所有的计算都在一个8核CPU上完成。

虽然GFN2-xTB是一个比DFT精确度低的理论方法，但是两种方法预测的最小化结构往往一致。如图5所示，使用GFN2-xTB和DFT-B3LYP/6-31G(d)最小化的葡萄糖，优化好的结构的全局全原子均方根偏差（RMSD）仅为0.93Å。

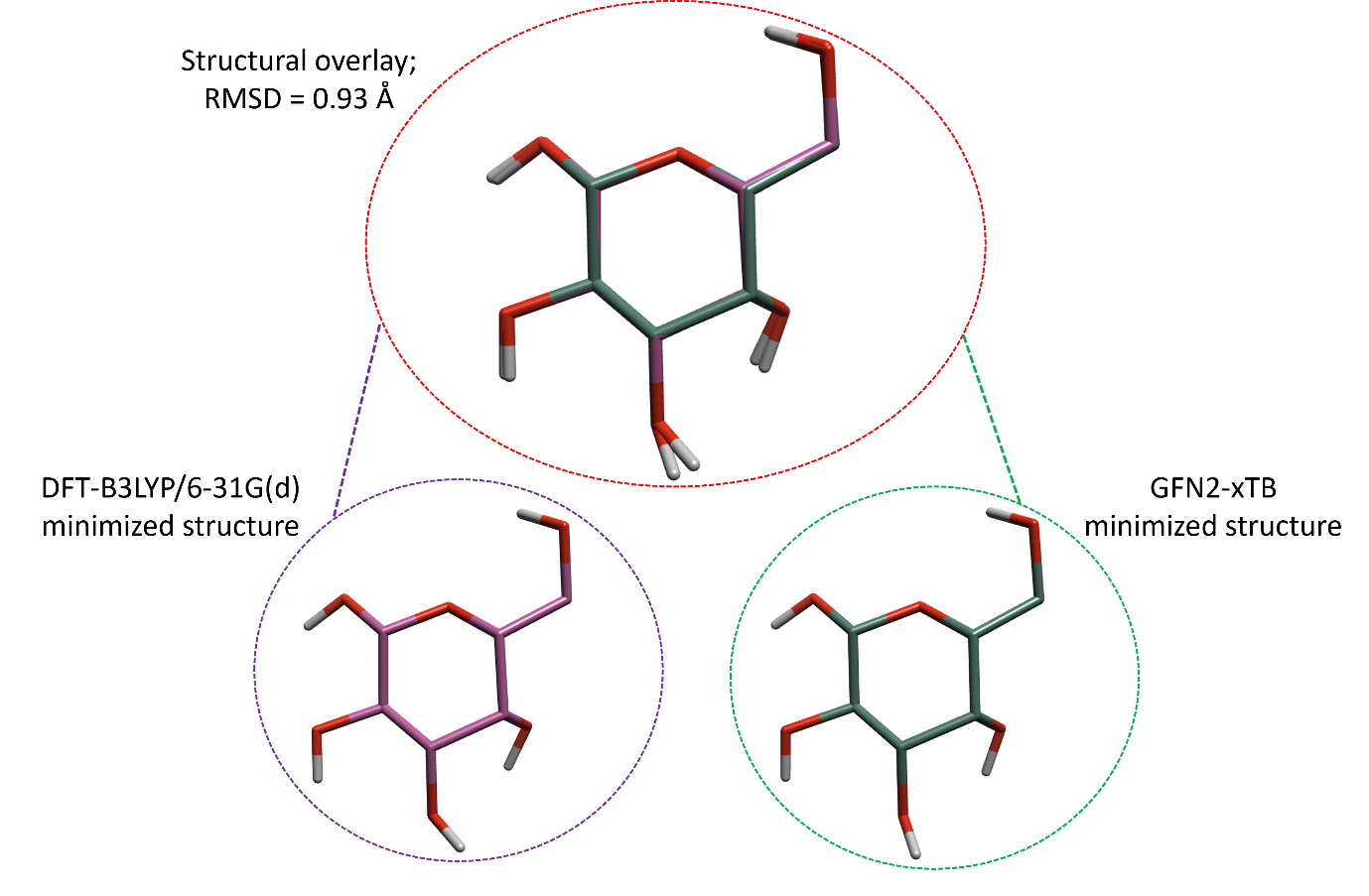
两个葡萄糖分子的结构叠合

图5. 两个葡萄糖分子的结构叠合，一个（左边，紫色）在B3LYP/6-31g(d)理论水平优化，另一个（右边，绿色）在GFN2-xTB理论水平优化

小结

在本文中，我们强调了GFN2-xTB作为一种更易于计算的方法在更大的（100多个原子）分子结构上执行最小化和单点能计算。该方法不仅因计算时间短而吸引人，而且采用了GFN2-xTB//DFT混合的最小化和单点能工作流可以在速度和精度之间达到最佳平衡。

联系我们，获取试用

想在自己的项目中使用QM计算，或者您想借此机会探索Flare及其完整的CADD功能组合，请立即联系我们，申请免费试用。

参考文献

  1. http://www.psicode.org
  2. Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-XTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15 (3), 1652–1671. https://doi.org/10.1021/acs.jctc.8b01176.
  3. https://xtb-docs.readthedocs.io/en/latest/setup.html