摘要：本文介绍了势能面与反应坐标的概念，以及势能面与结构、能量的关系。还讨论了结构、稳定性、反应性和选择性与能量之间的关系。

原文：Warren J. Hehre. Wavefunction Inc (January 1, 2003).
编译：肖高铿/2023-12-05

前言

每一位学过化学的人都会遇到过一个曲线图，如图1所示，它将乙烷的能量变化描述为碳-碳键扭转角的函数。

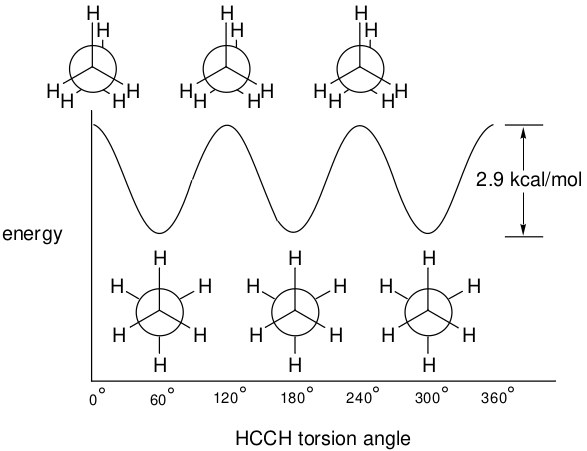
图1. 乙烷的势能面

完全360°旋转会之后会产生三个相同的交叉式（staggered）结构，它们是能量最小值的结构；还会产生三个完全相同的重叠式(eclipsed)结构，它们是能量最大值的结构。乙烷的重叠式结构和交叉式结构之间的能量差，称为旋转势垒，实验上已知为2.9kcal/mol（12kj/mol）。请注意，对乙烷的任何物理测量都只涉及其交叉式结构，或者更准确地说，是三个相同交叉结构的集合。也就是说，重叠式乙烷是不存在的，因为不可能将其分离出来或对其进行物理测量。相反，重叠式乙烷只是一种“想象”出来的、处于相同交叉式结构之间的结构。

更复杂但也更为大家熟悉的是正丁烷中心碳-碳键扭转角与能量的关系图，如图2所示。

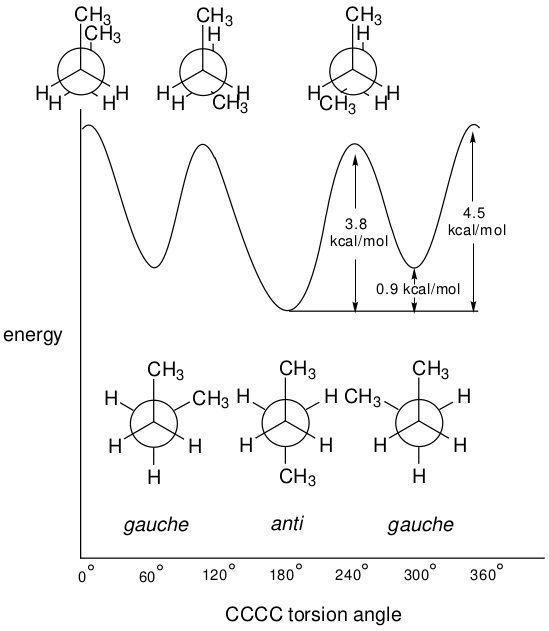
图2. 正丁烷的势能面

该图揭示了三个能量最小值，对应于交叉式结构；以及三个能量最大值，对应于重叠式结构。然而，在正丁烷的情况下，每组中的三种结构并不相同。其中一个最小值对应的扭转角为180°（anti-反式结构），其能量较低；另外两个最小值对应的扭转角约为60°与300°（gauche-扭转式结构），这两个极小值的能量是相同的。类似地，其中一个能量最大值对应的扭转角为0°，其不同于另外两个的能量最大值，它们具有相同的能量，对应的扭转角约为120°和240°。

与乙烷的情况一样，正丁烷的重叠式结构并不存在，只是一种对应于反式（anti-）极小值和扭转式(gauche-)极小值之间的、假设出来的结构。与乙烷不同，乙烷是一种单纯化合物，而任何正丁烷样品都由两种不同的化合物组成，即anti-正丁烷和gauche-正丁烷。这两种化合物的相对丰度是温度的函数由玻尔兹曼方程给出（见下文讨论）。

上述两个例子中的“重要”几何坐标可以清楚地确定为涉及一个特定碳-碳键的扭转。事实上，这过于简单化了，因为在围绕碳-碳键旋转的过程中，毫无疑问也会发生其他几何变化，例如键长和健角的变化。在这两个例子里，这种可能很小，可以安全地忽略。然而，并不总是能够找到这么一个“简单”的几何坐标。环己烷“环翻转”的势能面提供了一个很好的例子。

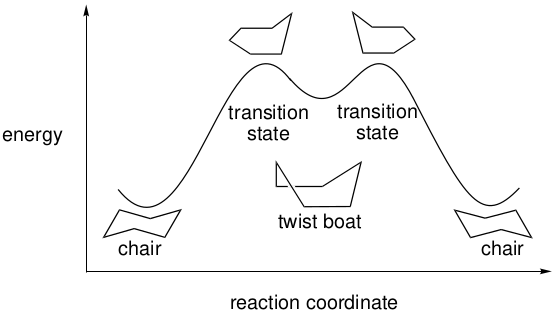
图3. 环己烷环翻转的势能面

与前面两个例子不同，在这个例子中没有详细地描述连接稳定形式的几何坐标，而是简称为“反应坐标”。此外，能量最大值被称为“过渡态”，这表明它们的结构可能无法像在乙烷和正丁烷中旋转的能量最大值那样简单的描述。

与正丁烷的势能面一样，环己烷环翻转的势能面了包含三个不同的能量极小值，其中两个较低能的结构为“椅式”，另一个较高能量的为“扭船式”。事实上，椅式和扭船式结构之间的能量差足够大，为5.5kcal/mol或23kJ/mol，在室温下椅式与扭船式对应的平衡比大于99:1，以至于在常温下只能观察到前者。

椅式环己烷的六个碳都是等价的，但氢分为两组，如图4所式，一组是六个等价的平伏键（equatorial）氢，另一组是六个等价的直立键（axial）氢。

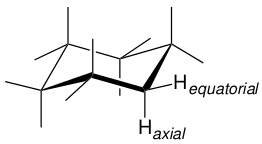
图4. 环己烷两组等价的氢原子

然而，通常只能观察到一种氢，这意味着平伏键和直立键位置可以通过低能量过程相互转换。这就是刚才描述的环翻转过程，如图5所示，其中环的一侧向上弯曲，而另一侧向下弯曲。

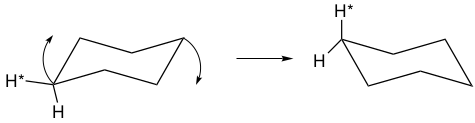
图5. 环己烷环的翻转

根据图4的势能图，以扭船式结构作为中间点（中间体），整个过程实际上分为两个步骤。该中间体有两个等价的过渡态结构，其中五个环碳近似位于一个平面上。

考虑到已经说过的正丁烷中单键旋转，环己烷中环翻转的能量分布可以合理化。基本上，椅式环己烷通过扭船式中间体的过渡态可以相互转化。这种相互转化可视为围绕其中一个环键的“受限旋转”。

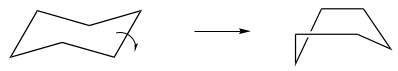
图6. 环己烷环的受限旋转

相应地，从扭船式中间体到另一种椅式的相互转换可以被视为围绕相反环键的旋转。总的来说，两个独立的“键旋转”暂停在高能但稳定法扭船式中间体，将一个椅式结构转换为另一个等价的椅式结构，同时切换平伏键与直立键方向上的氢。

乙烷、正丁烷和环己烷都提供了分子可能经历的运动类型的实例。它们的势能面是普通类型图的特例，如图7所示，其中能量是作为反应坐标的函数而给出的。

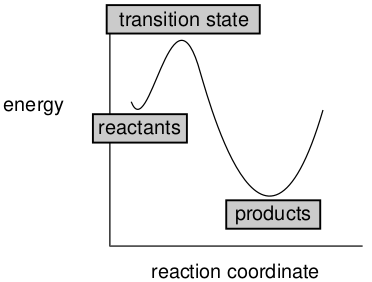
图7. 势能面是能量作为反应坐标函数而绘制的图

像图7这样的“反应坐标图”提供了化学可观测物——结构、稳定性、反应性和选择性——与能量之间的重要联系，接下来我门开始探讨这些联系。

势能面与几何

如图8所示，沿反应坐标能量最小值的位置给出了反应物和产物的平衡结构。类似地，能量最大值的位置给出了过渡态的结构。

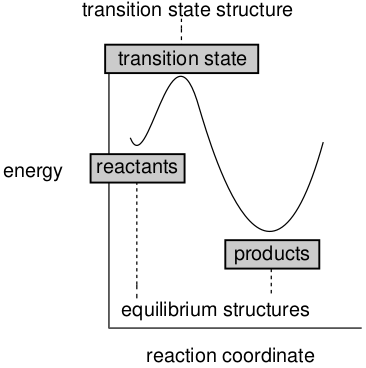
图8. 反应物、产物与过渡态

例如，当“反应”是围绕乙烷中的碳-碳键旋转时，反应坐标可以简单地认为是HCCH扭转角，而结构可以单独根据这个角度来确定。因此，交叉式乙烷（反应物和产物）是一个该角度为60°的分子，而重叠式乙烷是该角度为0°的分子。

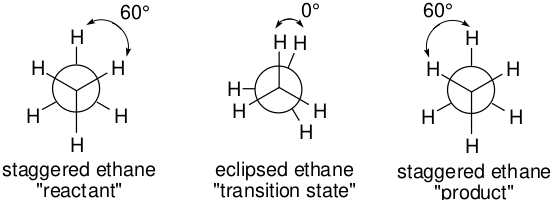
图9. 乙烷碳-碳键旋转与反应坐标

类似的描述适用于扭转式正丁烷的“反应”，从而产生更稳定的反式构象异构体。同样，反应坐标可以被认为是关于中心碳-碳键的扭转，以及在这个坐标上的单个反应物、过渡态和产物结构，见图10。

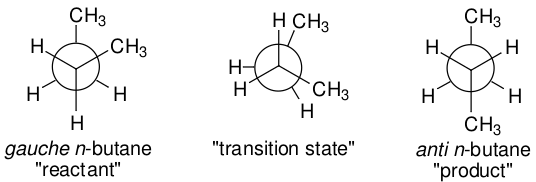
图10. 正丁烷碳-碳键旋转的反应物与反应物结构

平衡结构（几何结构）可以通过实验确定，前提是分子可以制备，并且足够长寿以便可以进行测量。请注意，当两种或两种以上结构共存时，例如，反式-正丁烷和扭转式-正丁烷，实验测量可以得到单一的“平均”结构或者是两个结构的“复合”结构。过渡态的几何结构可能无法通过实验测量确定。这仅仅是因为就可以进行测量的分子布局数（Population）而言，过渡态并不“存在”。

平衡态结构和过渡态结构都可以通过计算来确定。前者需要在势能面上搜索能量最小值，而后者需要搜索能量最大值。寿命甚至存在性都不是必要条件。

势能面与热力学

反应物和产物的相对稳定性通过它们在势能面上的相对高度来指示，这给出了反应的热力学，如图11所示。

图11. 反应热力学

严格来说，这并不完全正确。因为热力学取决于反应物和产物的相对自由能。自由能（ΔG）由焓（enthalpy，∆H）减去熵（entropy，∆S）和绝对温度的乘积得出：

ΔG = ΔH - TΔS

而在焓与能量之间有个差值：

ΔH = ΔE - Δ(PV)

在正常情况下我们可以安全地忽略差值Δ(PV) 。尽管对于许多重要类型的化学反应来说，与焓的贡献相比，熵的贡献通常非常小，但是我们不能忽略熵对自由能的贡献。为了方便讨论，在本文中将自由能和能量同等对待。

在乙烷中键旋转的情况下，“反应物”和“产物”是相同的，该反应被称为“热中性”。环己烷的整个环翻转运动也是如此。

更常见的情况是，如上图11所示，产物的能量低于反应物的能量。这种反应被称为放热反应，反应物和产物稳定性的差异仅仅是它们的能量差异。例如，扭转式-正丁烷与反式-正丁烷的“反应”是放热的，两种构象的稳定性差异仅仅是它们在能量上的差异（0.9 kcal/mol或3.8kJ/mol）。

热力学告诉我们，如果我们等待足够长的时间，放热反应中产物的量将大于反应物（起始原料）的量。产物与反应物的实际比例也取决于温度，并由玻尔兹曼方程给出。

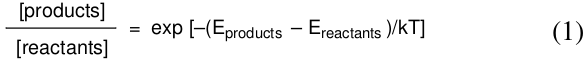
这里，E_products和E_reactants是势能图上产物和反应物的能量，T是温度（Kelvin），k是玻尔兹曼常数。玻尔兹曼方程告诉我们，在无限的时间内，产物和反应物的相对量，[products]/[reactants]。

由此我们可以推知，即使主产物与副产物在能量上非常小的差异也会导致巨大的产物比例，见表1。

表1. 主产物与副产物比例与能量差的关系

ΔE（kcal/mol）	ΔE（kj/mol）	product ratio(major:minor)
0.5	2	80:20
1	4	90:10
2	8	95:5
3	12	99:1

化学反应也可以是吸热的，其反应曲线如下图12所示。

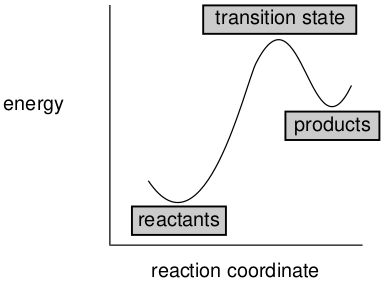
图12. 吸热化学反应

在这种情况下，最终会有更多的反应物而不是产物。

在一个反应中可能形成两种或多种不同产物的情况下，热力学告诉我们，如果我们等待足够长的时间，无论反应路径如何，形成的最大丰度的产物都将是能量最低的产物。

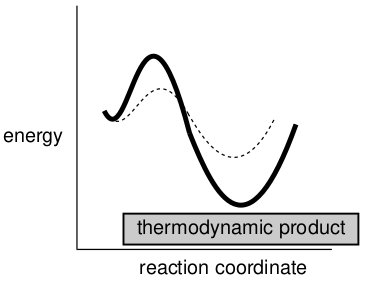
图13. 热力学控制的反应

在这种情况下，产物被称为“热力学产物”，反应被称为是“热力学控制的反应”。

势能面与动力学

势能面还揭示了有关反应发生的速度或速率的信息，这就是反应动力学。

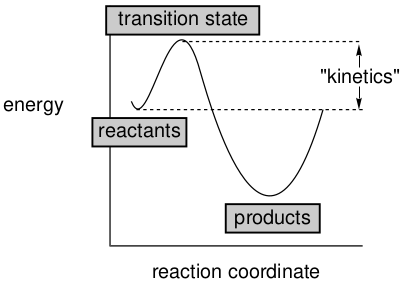
图14. 反应动力学

绝对反应速率不仅取决于反应物的浓度[A]^a、[B]^b...，其中a、b…通常是整数或半整数，并且还取决于一个被称为速率常数的量。

rate = rate constant[A]^a[B]^b[C]^c... （2）

速率常数由取决于温度的阿伦尼斯方程给出。

rate constant = A*e^{-(E_{transition state}-E_reactants)/RT} （3）

除了温度，速率常数还取决于压力，但通常被忽略压力因素。

这里，E_{transition state}和E_reactants分别是过渡态和反应物的能量，T是温度，R是气体常数。注意，速率常数（以及总速率）不取决于反应物和产物的相对能量（“热力学”），而仅取决于反应物和过渡态之间的能量差。这种差异通常被称为活化能或能垒，通常用符号∆E^‡表示。其他因素，如分子之间相遇的可能性和这些相遇促进反应的有效性，通过“A因子”乘以指数的方式加以考虑。对于涉及单一反应物生成不同产物的反应，或涉及密切相关反应物的反应，通常假定这是常数。

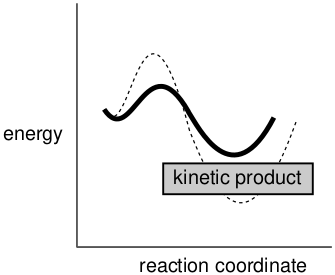
图15. 动力学产物

动力学产物比率显示出与活化能差异的相关性，活化能差异与反应物和产物能量差异的热力学产物比率相同，见表1。

化学反应的热力学与动力学控制

事实上，有两种不同且独立的机制控制产物分布——热力学和动力学——这就是为什么一些化学反应在一组条件下产生一种产物分布，而在另一组条件下产生完全不同的产物分布。这也解释了为什么有机化学家允许一些反应“煮”几个小时，而另一些反应刚开始几秒钟后就急着“熄灭”。

根据图16的反应坐标图，这是一个从单一反应物(或一组反应物)开始并产生两种/组不同产物的过程。

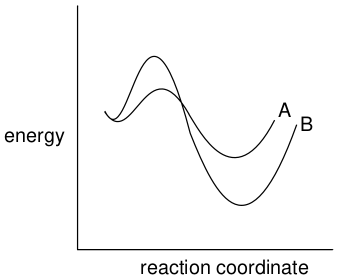
图16. 一个反应两个/组产物的反应

根据图16，路径A通过较低能量的过渡态产生较高能量的产物，是动力学产物有利的反应路径，生成动力学产物。路径B通过较高能量的过渡状态进行，但生成较低能量的产物。这是热力学有利的反应路径，生成热力学产物。通过改变反应条件（温度、反应时间、溶剂），化学家可以影响产物的分布。

当然，反应坐标图也可能是动力学和热力学产物相同的，如图17所示，路径B既是动力学路径又是热力学路径，其产物既是动力学产物又是热力学产物。

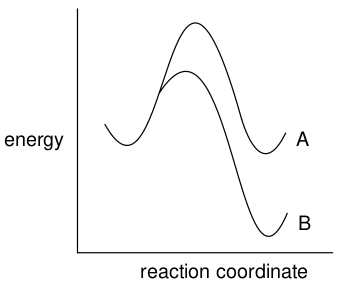
图17. 产物B既是动力学产物又是热力学产物

在这里，反应条件的变化也会影响产物分布，因为活化能的差异与产物能量的差异可以是不同的。

任何给定化学反应的产物的确切分布取决于反应条件；“持续烹煮”，即较长的反应时间，会产生热力学产物分布，而“快速淬火”则产生动力学分布。

自由基环化反应是动力学和热力学产物不同的一个很好的例子。5-己烯自由基的环化可以产生环戊基甲基自由基或环己基自由基，如图18所示。

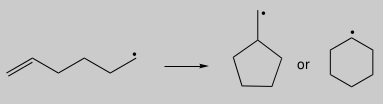
图18. 5-己烯自由基的环化

虽然环己基在热力学上比环戊基甲基更稳定，一方面六元环比五元环的张力能更小，另一方面2˚-自由基比1˚-自由基更受具有优势，但环戊基甲基形成的产物占主导地位，例如图19的反应。

图19.1-溴-5-己烯自由基环化

基于QM的计算表明，环己基比环戊基甲基更稳定，能量低了约8kcal/mol。如果反应在严格的热力学控制下，则根本不应观察到来自环戊基甲基自由基的产物。然而，与自由基攻击“内”双键碳（导致环戊基甲基自由基）相对应的过渡态的能量比与自由基吸引对“外”双键碳（导致环己基自由基）对应的过渡态低了约3kcal/mol。这意味着主产物与次产物（有利于生成环戊基甲基的产物）的比例约为99:1，与实际观察到的结果一致。反应显然处于动力学控制之下。

势能面与反应机理

真正的化学反应不一定一步完成，而是可能涉及几个不同的步骤以及一个或多个中间体。整个步骤序列称为一个机理，可以用反应坐标图来表示。

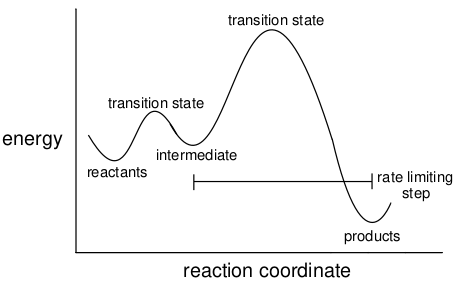
图20.用反应坐标表示反应机理

反应的热力学如前所述，即与反应物和生成物之间的能量差有关，中间体不起任何作用。然而，反应动力学的正确解释确实需要考虑所有步骤和所有过渡态。当一个过渡态的能量比其他任何一个都高时，如上图20所示，总体动力学可以安全地假设仅依赖于这个“限速步骤”。

原则上，可以通过计算建立机理，只需首先阐明从反应物到产物的所有可能序列，然后确定具有“最快”限速步骤的特定序列，即具有最低能限速过渡态的特定序列。这还不是普遍的做法，但可以这么作。如果发生这种情况，计算将为阐明反应机理的实验提供有力的补充。

参考文献

1. Warren J. Hehre. Wavefunction Inc (January 1, 2003). A Guide to Molecular Mechanics and Quantum Chemical Calculations.