摘要：在本文中，我们用计算构象预组织（conformational pre-organization）分析了活性跨度为2个数量级的4个大环CDK2抑制剂分子，预期构象系综内的活性构象比例高的化合物比活性构象比例低的化合物具有更高的结合亲和力。结果表明，活性构象比例与结合自由能ΔGbinding（根据IC50计算而来）具有显著的线性关系，Pearson线性相关性系数R2=0.99，完美地对这4个不同连接臂的大环CDK2抑制剂进行优先级排序，初步证明了方法的可靠性。该方法计算简便、原理可靠，有望发展为大环化合物优先级排序的强大工具。

作者：肖高铿
日期：2024-05-14

背景

此前，我们用Spark的大环化合物设计工作流重现了Yu等人1报道的大环CDK2抑制剂QR-6401的设计2。然而，由于大环化合成的成本很高，在现实的药物发现项目中，希望在合成之前能够对这些设计的大环化合物进行优先级排序，尽量将最有价值的设计排序靠前。因此，本文的目的是以其中4个化合物为例（见图1），演示如何用之前所述的计算构象预组织方法3来对这些大环化合物进行排序，初步证明这个方法的可靠性。

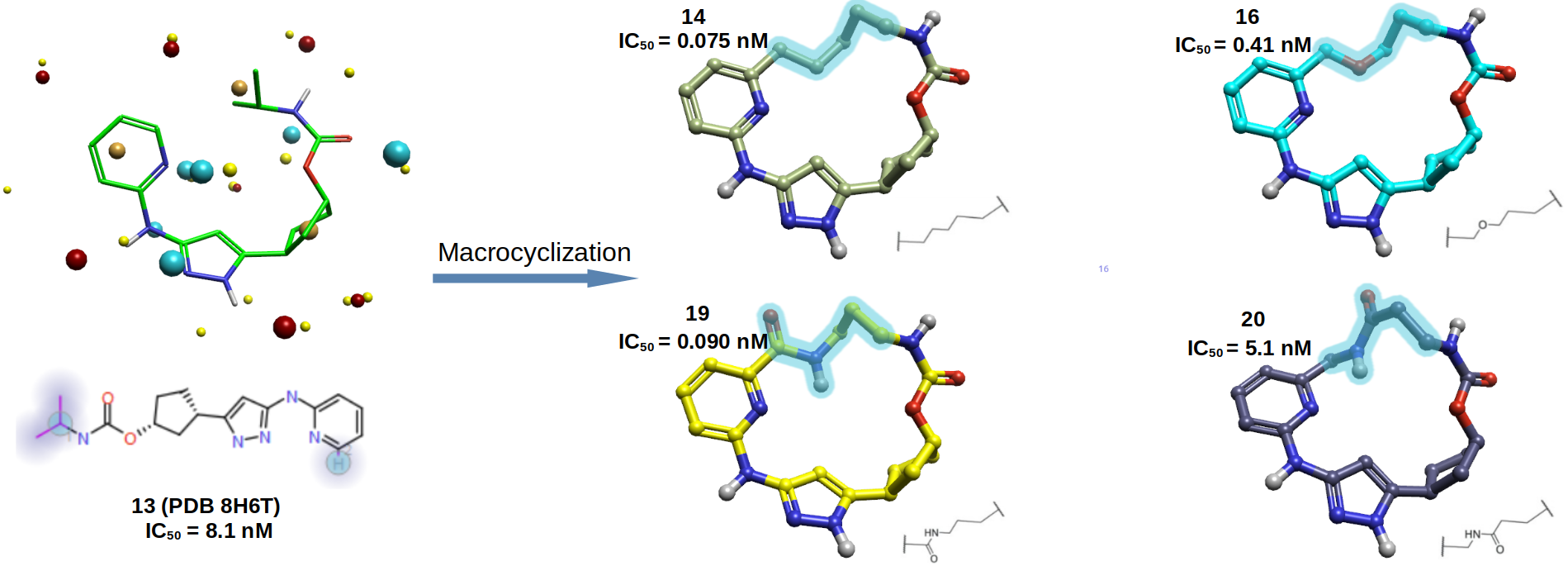
some macrocyclic cdk2 inhibitors:化合物13的大环抑制剂设计

图1. Yu等人1报道的线型化合物13及其大环CDK2抑制剂

结果

大环CDK2抑制剂构象系综的计算

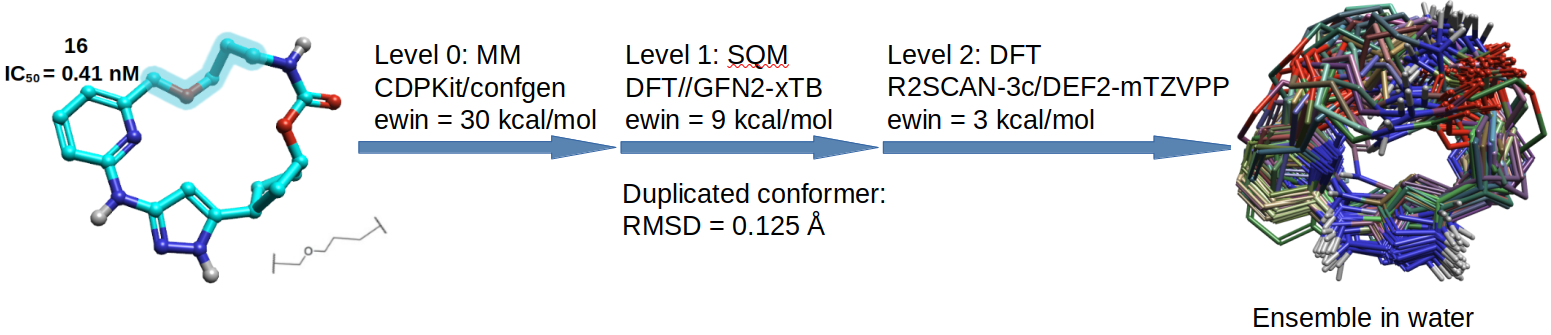
ReSCoSS工作流计算构象系综

图2. 用Udvarhelyi等人4提出的ReSCoSS工作流计算构象系综

用Udvarhelyi等人4提出的ReSCoSS工作流（略有改动）来计算14、16、19、20在水溶液中的构象系综，如图2所示，分三个步骤分别在三种不同的理论级别方法上计算完成：

  1. Level_0：MMFF94

    2. 用CDPKit软件包的confgen5,6生成构象，其中用MMFF94力场评估构象能，用RMSD=0.5作为重复构象的阈值，保留构象能\(\le \)30kcak/mol的构象，得到初始的构象系综。

  2. Level_1：R2SCAN-3c/DEF2-mTZVPP//GFN2-xTB

    3. 以Level_0的构象系综为输入，在GFN2-xTB理论水平7,8下进行几何优化，用RMSD=0.125Å作为重复构象的阈值进行构象去重。然后用Spicher与Grimme等人16的单点Hessian法（Single Point Hessian）计算每个构象的自由能G，参见方法部分式4。其中\(E^{DFT}_{water}\)是在R2SCAN-3c/DEF2-mTZVPP/IEFPCM-water理论水平9单点能计算得到的电子结构能量；\(G_{mRRHO}\)是用xTB在GFN2-xTB/alpb-water理论水平计算熵对自由能的贡献。最后保留\(G\le \)9kcak/mol的构象，得到新的构象系综。

  3. Level_2：R2SCAN-3c/DEF2-mTZVPP/IEFPCM-Water

    4. 以Level_1的构象系综为输入，在R2SCAN-3c/DEF2-mTZVPP/IEFPCM-Water理论水平9下进行几何优化；然后在R2SCAN-3c/DEF2-mTZVPP/IEFPCM-water理论水平9下进行单点能计算，得到构象的电子结构能量\(E^{DFT}_{water}\)；在GFN2-xTB/alpb-water理论水平计算熵的贡献（\(G_{mRRHO}\)）；根据式4得到构象自由能G，保留\(G\le \)3kcak/mol的构象，得到最终的构象系综。

这是一个构象数递减、精度逐步提高的过程，这么做的主要目的是尽可能地减少计算量，而精度损失较小。结果如表1所示，随着计算的进行，系综的构象数越来越少。

表1. 在不同理论级别下计算得到的构象系综的大小

Method 13 14 16 19 20
Level_0 – 547 484 471 474
Level_1 – 477/243 369/151 322/81 315/121
Level_2 – 80 60 28 20

其中level_1构象数：聚类前/聚类后

构象系综与活性

用Flare Conf & align或pyflare align.py脚本10将14、16、19、20的水溶液构象系综根据场相似性叠合到参比分子13上。因为大环化合物与参比分子的大小不同，因此使用Tversky为相似性指标，并且偏向参比分子，因此设置Tversky的α=0.95。定义Tversky Sim\(\ge\)0.75的构象作为活性构象，统计构象系综中\(ΔG\le 2.5kcal/mol\)（96%构象空间）的活性构象比例，结果如表2所示。

表2. 化合物的构象分布与结合自由能

Compound Proportion of Bio-Confs. \(\langle Tversky Sim\rangle\) ΔGbinding (kcal/mol)
13 – – -11.03
14 72.5% 0.735 -13.80
16 57.2% 0.738 -12.80
19 67.8% 0.748 -13.69
20 39.1% 0.709 -11.30


可以看到，化合物14、16、19、20水溶液构象系综中的活性构象比例与结合自由能ΔGbinding（根据IC50计算而来）具有显著的线性相关性，Pearson相关性系数\(R^2=0.99\)，如图3所示。需要注意的是，这个相关性并不具备严格的统计学意义，一方面因为数据点太少，另一方面因为活性跨度最大才两个数量级，所以有待在更大规模的数据集上进行测试。

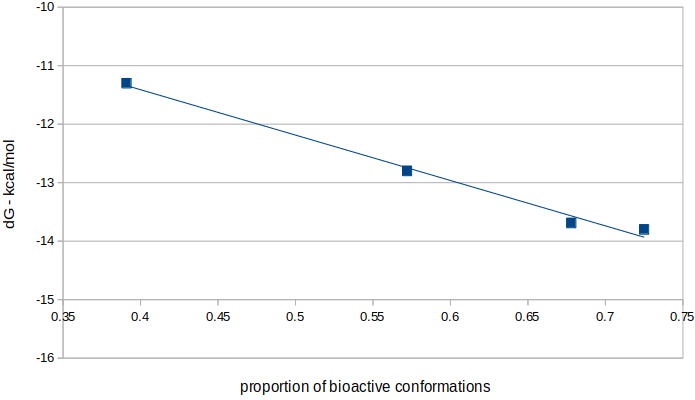
活性构象比例与结合自由能的具有显著的线性关系

图3. 活性构象比例与结合自由能ΔGbinding具有显著的线性关系，Pearson线性相关性系数\(R^2=0.99\)

活性构象比例的计算方法有多种变体，比如在Sindhikara等人12的研究中，先计算构象与参比分子公共子结构的RMSD，然后计算波尔兹曼加权平均RMSD，即\(\langle RMSD\rangle\)，并作为活性构象比例的替代指标，预期\(\langle RMSD\rangle\)越小，活性越强。受此启发，考察了波尔兹曼加权平均Tversky相似性，即\(\langle Tversky Sim\rangle\)，预期该值越大，活性越强。结果如表2所示，\(\langle Tversky Sim\rangle\)与活性貌似没有预期的趋势关系。

方法

大环构象生成

CDPKit的confgen5,6用来搜索大环的初始构象。

QM计算

GFN2-xTB与DFT几何优化、单点能计算采用pyflare脚本qm.py10完成。化合物的构象熵采用独立版本的xTB（Version 6.7.0）7, 8在alpb模型的水溶液环境下计算。

波尔兹曼权重

构象系综中每个构象的波尔兹曼权重根据构象的自由能（G）计算，将能量最低的构象定为零点取相对值(ΔG)，根据平衡常数与自由能变的关系可以得到：

$$
q = e^{-ΔG \over {RT}}\cdots (1)
$$

其中R为气体常数，T为温度。构象i出现的概率（Pi）服从玻尔兹曼分布：

$$
P_i = {q_i \over \sum{q_i}}\cdots (2)
$$

构象自由能

构象自由能G是根据Spicher等人11的单点Hessian（Single Point Hessian，SPH）方法计算，将电子结构能量与熵贡献根据相加得到：
$$
G = {E^{DFT}_{water} + G^{GFN2-xTB/alpb-water}_{mRRHO}}\cdots (3)
$$

其中\(E^{DFT}_{water}\)，比如在Level_2时，是在R2SCAN-3c/DEF2-mTZVPP/IEFPCM-Water理论水平计算的电子结构能量，已经包含了溶剂效应。其中\(G_{mRRHO}\)是熵对自由能贡献，是根据SPH法在GFN2-xTB/alpb-water理论水平计算的，也已经包含了溶剂效应。

构象叠合与3D-相似性计算

用pyflare脚本align.py10将构象系综叠合到参比分子上，设置相似性算法用Tversky，α=0.95以偏好于参比分子。

对于具有k个构象的构象系综，波尔兹曼加权平均TerskySim值由下式4给出：

$$
\langle Tversky Sim\rangle = \sum\limits_{i=1}^{k}P_{i}\times TverskySim_{i}\cdots(4)
$$

其中Pi为构象i的波尔兹曼权重，由方程（2）计算得到；TverskySimi是构象i与参比分子之间的Tversky（α=0.95）相似性。

结论

在本文中，我们用计算构象预组织分析了活性跨度为2个数量级的4个大环CDK2抑制剂分子，预期构象系综内的活性构象比例高的化合物比活性构象比例低的化合物具有更高的结合亲和力。结果表明，活性构象比例与结合自由能ΔGbinding（根据IC50计算而来）具有显著的线性关系，Pearson线性相关性系数\(R^2=0.99\)，完美地对这4个不同连接臂的大环CDK2抑制剂进行优先级排序，初步证明了方法的可靠性。该方法计算简便、原理可靠，有望发展为大环化合物优先级排序的强大工具。

此外，在此过程中，我们得到了大环化合物的构象系综，可以进一步计算油/水溶剂转移自由能用来评估细胞膜渗透性13，这对于需要透过血脑屏障的项目特别有益。

文献

  1. Yu, Y.; Huang, J.; He, H.; Han, J.; Ye, G.; Xu, T.; Sun, X.; Chen, X.; Ren, X.; Li, C.; et al. Accelerated Discovery of Macrocyclic CDK2 Inhibitor QR-6401 by Generative Models and Structure-Based Drug Design. ACS Med. Chem. Lett. 2023. https://doi.org/10.1021/acsmedchemlett.2c00515.
  2. 用SPARK重现选择性大环CDK2抑制剂QR-6401的设计. http://blog.molcalx.com.cn/2023/02/26/using-spark-to-design-macrocycle-cdk2-inhibitors.html
  3. 用计算方法研究大环分子的构象预组织——BCL6抑制剂的案例分析. http://blog.molcalx.com.cn/2024/05/06/bcl6-inhibitor-macrocylization.html
  4. Udvarhelyi, A., Rodde, S. & Wilcken, R. ReSCoSS: a flexible quantum chemistry workflow identifying relevant solution conformers of drug-like molecules. J Comput Aided Mol Des. 2021,35,399–415. https://doi.org/10.1007/s10822-020-00337-7
  5. CDPKit Version 1.1.0. https://github.com/molinfo-vienna/CDPKit
  6. Seidel, T. et al. (2023) “High-Quality Conformer Generation with CONFORGE: Algorithm and Performance Assessment,” Journal of Chemical Information and Modeling, 63(17), pp. 5549–5570. Available at: https://doi.org/10.1021/acs.jcim.3c00563.
  7. xTB Version 6.7.0. Semiempirical Extended Tight-Binding Program Package. https://github.com/grimme-lab/xtb
  8. Bannwarth, C. et al. (2021) “Extended tight-binding quantum chemistry methods,” Wiley Interdisciplinary Reviews: Computational Molecular Science. Blackwell Publishing Inc. Available at: https://doi.org/10.1002/wcms.1493.
  9. Grimme, S. et al. (2021) “R2SCAN-3c: A ‘swiss army knife’ composite electronic-structure method,” Journal of Chemical Physics, 154(6). Available at: https://doi.org/10.1063/5.0040021.
  10. Flare V8.0. http://www.cresset-group.com/software/flare
  11. Spicher, S. and Grimme, S. (2021) “Single-Point Hessian Calculations for Improved Vibrational Frequencies and Rigid-Rotor-Harmonic-Oscillator Thermodynamics,” Journal of Chemical Theory and Computation, 17(3), pp. 1701–1714. Available at: https://doi.org/10.1021/acs.jctc.0c01306.
  12. Sindhikara, D. and Borrelli, K. (2018) “High throughput evaluation of macrocyclization strategies for conformer stabilization,” Scientific Reports, (April), pp. 1–8. Available at: https://doi.org/10.1038/s41598-018-24766-5.
  13. Kamenik, A.S. et al. (2020) “Macrocycle Cell Permeability Measured by Solvation Free Energies in Polar and Apolar Environments,” Journal of Chemical Information and Modeling, 60(7). Available at: https://doi.org/10.1021/acs.jcim.0c00280.

联系我们、获取试用或商务合作

想要亲自计算或在自己的项目中使用Flare或Spark，或者商务合作，请联系我们。