计算大环ALK抑制剂的全局构象张力能
摘要:本文以大环ALK抑制剂Lorlatinib发现过程中活性差异20倍的一个分子对为例,演示了它们的构象张力能计算以评估其结合构象的稳定性。结果表明,计算的结合构象张力能与文献报道的FEP+方法一样,预测的结合自由能差值非常接近实验的结合自由能差值。这说明,在连接臂没有参与蛋白相互作用情况下,假设线型先导化合物与大环化合物之间的活性差异是由它们之间的构象张力能差异引起的,通过计算结合构象的张力能可以评估大环化合物是否比线型衍生物具有更好的构象稳定性从而具有更高的活性。
作者:肖高铿/2024-05-31
前言
Garcia等人1的最近研究表明,与相比线型小分子化合物相比,大环化合物具有多种优点,比如高结合亲合力、靶标选择性、更好的DMPK性质。比如,难以用传统小分子药物靶向的具有平坦或浅平结合位点的靶标,大环药物比其线型药物的亲和力可以达到高达100倍的增加,大环可以产生非常适合的候选药物。尽管大环药物的分子量较大,但其具有足够的生物利用度以在口服给药后达到细胞内靶标。在Garcia等人1统计的大环药物中,40%具有足够的口服生物利用度。
然而,大环化合物由于难以合成,因此有必要在合成之前采用计算方法进行优先级排序。此前,我们介绍了如何用FreeForm2计算全局构象张力能来评估线型先导化合物与大环化合物的构象稳定性来进行优先级排序3。后来又介绍了计算构象预组织(Conformational preorganization)方法,用来评估大环BCL6抑制剂的构象稳定性4,对不同的大环CDK2抑制剂连接臂进行优先级排序5。
构象预组织指的是药物分子在未与生物靶标结合时,已经处于或者能够容易地达到一个构象状态,这个状态与它在结合时的生物活性构象相似或一致6。一个预组织的分子可能会在结合时经历较小的构象变化,因此需要的能量(reorganization energy,重组能量)也较小。重组能量(reorganization energy)6指药物分子从其自由状态(未结合状态)转变为与生物靶标结合的状态时所需吸收或释放的能量。这个能量变化涉及到药物分子内部结构的调整,包括原子间距离、键角、二面角的变化,以及内部非共价相互作用的重新分布。重组能量在蛋白-配体结合时也称为构象能惩罚(conformational energy penalty)7或者张力能(strain energy)8。
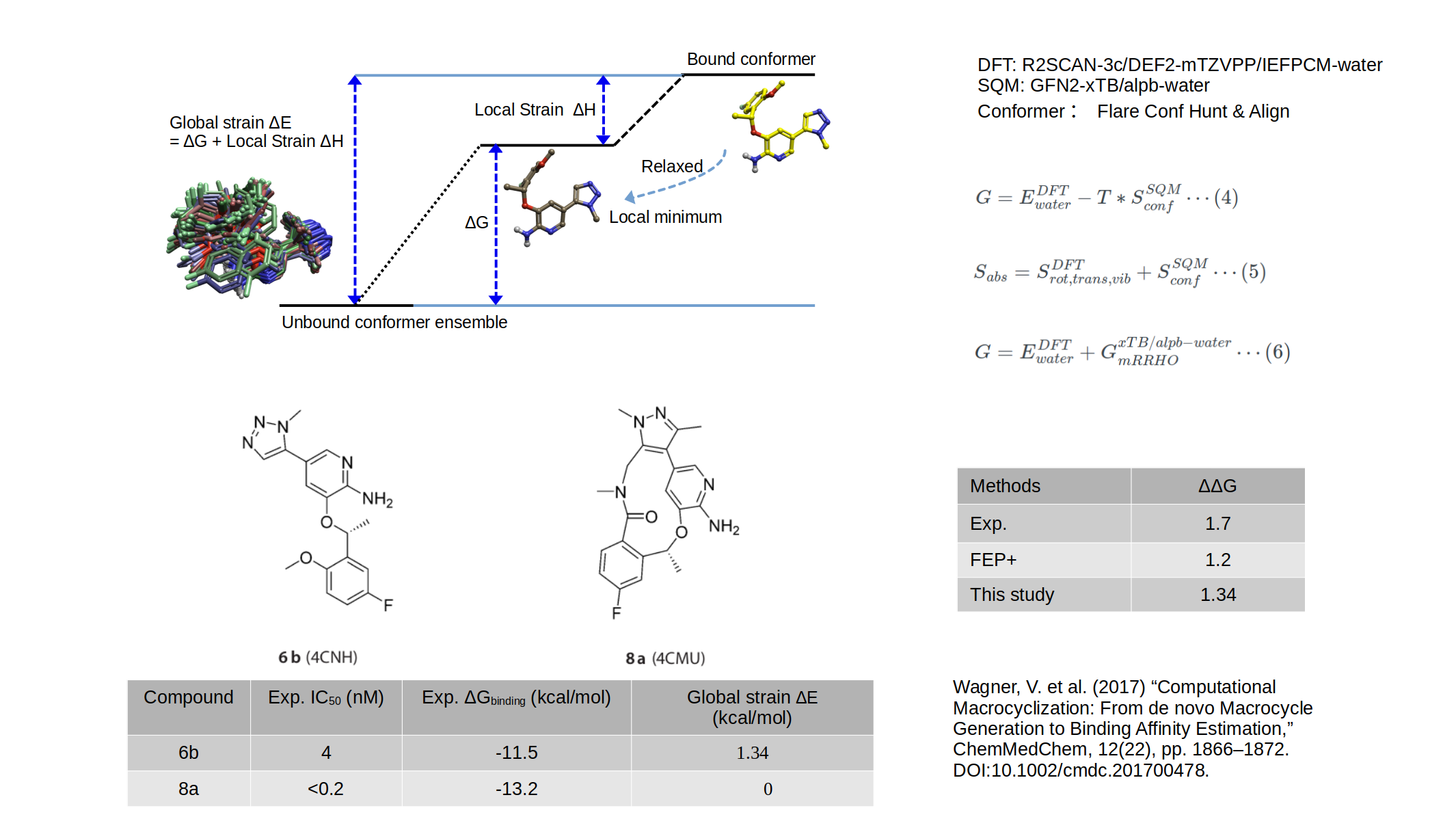
在连接臂没有参与蛋白的相互作用情况下,我们可以假设线型先导化合物与大环化合物之间的活性差异是由它们之间的构象张力能差异引起的,因此通过计算结合构象的张力能可以评估大环化合物是否比线型衍生物具有更好的构象稳定性,从而具有更高的活性。本文以大环ALK抑制剂Lorlatinib(PF-06463922)发现过程中活性差异20倍的一个分子对6b与8a(图1)为例9,来演示它们的构象张力能计算以评估其结合构象的稳定性。这对分子也被用来评估炼金术结合自由能计算方法FEP+计算大环抑制剂相对结合自由能的性能10。本文的结果表明,计算结合构象张力能与FEP+方法可以得到几乎同样的结果,但前者计算起来更加便捷。
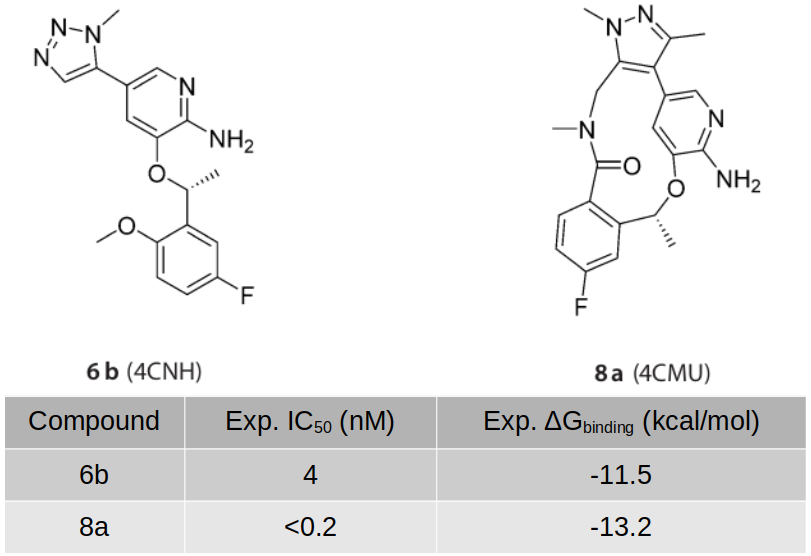
图1. ALK抑制剂分子对线型化合物6b与大环化合物8a的化学结构
结果
水溶液构象系综的计算

图2. ReSCoSS构象系综计算工作流
用Udvarhelyi等人11提出的ReSCoSS工作流(略有改动)来计算6b与8a在水溶液中的构象系综,如图2所示,分三个步骤分别在三种不同的理论级别方法上计算完成:
- Level_0:XED
- Level_1:R2SCAN-3c/DEF2-mTZVPP//GFN2-xTB
- Level_2:R2SCAN-3c/DEF2-mTZVPP/IEFPCM-Water
用Flare V812的Conf Hunt搜索化合物构象,用RMSD=0.5Å作为重复构象的阈值,保留构象电子结构能量\(\le 30\)kcal/mol的构象,得到初始的构象系综。
以Level_0的构象系综为输入,在GFN2-xTB理论水平13,14下进行几何优化,用RMSD=0.125Å作为重复构象的阈值进行构象去重。然后根据Spicher与Grimme等人16的单点Hessian法(Single Point Hessian)计算构象自由能G:
$$
G = {E^{DFT}_{water} + G^{GNF2-xTB/alpb-water}_{mRRHO}}\cdots (1)
$$
其中\(E^{DFT}_{water}\)是在R2SCAN-3c/DEF2-mTZVPP/IEFPCM-Water理论水平15采用单点能计算得到的电子结构能量;GmRRHO是用xTB在GFN2-xTB/alpb-water理论水平计算的熵对自由能的贡献。最后保留\(G\le \)9kcal/mol的构象,得到新的构象系综。
以Level_1的构象系综为输入,在R2SCAN-3c/DEF2-mTZVPP/IEFPCM-Water理论水平15下进行几何优化,并在同一理论级别单点能计算得到构象的电子结构能量\(E^{DFT}_{water}\);接着用xTB在GFN2-xTB/alpb-water理论水平计算熵对自由能的贡献(GmRRHO);然后根据式1将两者加和得到构象自由能G,保留\(G\le \)3kcal/mol的构象,得到最终的构象系综。
需要注意的是,在DFT水平几何优化之后可能会出现构象合并,需要根据需要进行构象去重。
这是一个构象数递减、精度逐步提高的过程,这么做的主要目的是尽可能地减少计算量,而精度损失较小。结果如表1所示,随着计算的进行,系综的构象数越来越少。
表1. 在不同理论级别下计算得到的构象系综的大小
| Methods | 6b | 8a |
|---|---|---|
| Level_0 | 450 | 4 |
| Level_1 | 180/167 | 3/2 |
| Level_2 | 33 | 2 |
其中level_1构象数:DFT优化前/DFT优化后
构象张力能的计算
生物活性构象不一定是极小点,当不是极小点时不能直接计算构象熵而得到构象自由能,因此,采用图3的方法计算结合构象的张力能。
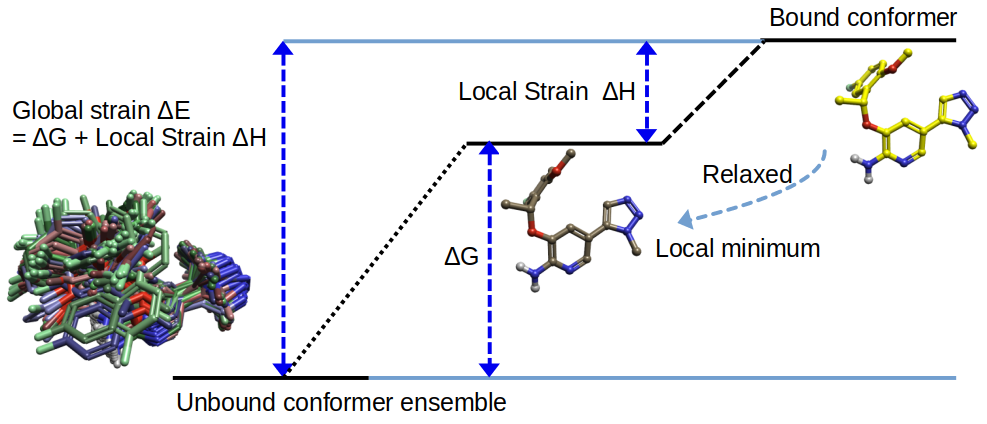
图3. 构象张力能的计算
对生物活性构象约束两面角,仅对键长、键角进行几何优化,计算电子结构能量Ebound;对生物活性构象进行几何优化,得到最近的极小点(local minimum),计算电子结构能量Elocal minimum,并以构象系综为参比计算构象自由能ΔG。
结合构象的全局张力能(Global Strain ΔE):
$$
Global\ Strain\ ΔE = ΔG + Local\ Strain\ ΔH \cdots (2)
$$
其中Local Strain ΔH:
$$
Local\ Strain\ ΔH = E_{bound} – E_{local\ minimum} \cdots (3)
$$
在本研究中,由于6b、8a在DFT理论水平几何优化的构象与生物活性构象的RMSD非常小,分别为0.40与0.26Å,因此可以近似地认为生物活性构象就是全局极小点,它们的Local Strain ΔH也近似为0kcal/mol。最终的全局构象张力能计算结果如表2所示。
表2. 6b与8a的全局构象张力能
| Items | 6b | 8a |
|---|---|---|
| Relaxed Bioactive ΔG | 1.34 | 0 |
| Local Strain ΔH | 0 | 0 |
| Global Strain ΔE | 1.34 | 0 |
| Exp. ΔG9 | -11.5 | -13.2 |
单位: kcal/mol;其中\(Exp. \ ΔG = RTlnIC_{50}\)
我们可以发现,6b比8a的全局构象自由能高了1.34 kcal/mol,这比Wagner等人10采用FEP+计算的结合自能差值(ΔΔG=1.2 kcal/mol)稍稍更加接近实验结合自由能差值(ΔΔG=1.7 kcal/mol),如表3所示。
表3. 6b与8a的计算与实验的ΔΔG值
| Methods | ΔΔG |
|---|---|
| This study | 1.34 |
| FEP+10 | 1.2 |
| Exp. 9 | 1.7 |
单位: kcal/mol
方法
构象搜索
使用Flare V8的Python API脚本confhunt.py对化合物6b与8a进行构象搜索。以6b为例:
1 2 3 4 | pyflare confhunt.py -i sdf -o sdf --exhaustive --energy-window 30 \
--filter 0.5 --maxconfs 2000 \
--dynamics-runs 20 \
--coulombics 6b.sdf >> ensemble.sdf |
QM计算
在GFN2-xTB与DFT理论水平的几何优化、单点能计算采用Flare V8的Python API脚本qm.py完成。构象的熵贡献(GmRRHO)采用独立版本的xTB(Version 6.7.0)13,14在GFN2-xTB/alpb-water理论水平计算。
结论
本文以大环ALK抑制剂Lorlatinib发现过程中活性差异20倍的一个分子对为例,演示了它们的构象张力能计算以评估其结合构象的稳定性。结果表明,计算的结合构象张力能与文献报道的FEP+方法一样,其预测的6b、8a分子对结合自由能差值(本文与文献FEP+的ΔΔG分别为1.34、1.20kcal/mol)非常接近实验结合自由能差值(ΔΔG=1.70kcal/mol)。这说明,在连接臂没有参与蛋白相互作用情况下,假设线型先导化合物与大环化合物之间的活性差异是由它们之间的构象张力能差异引起的,通过计算结合构象的张力能可以评估大环化合物是否比线型衍生物具有更好的构象稳定性而具有更高的活性,这可用于大环化合物合成的优先级排序。
文献
- Garcia Jimenez, D., Poongavanam, V. and Kihlberg, J. (2023) “Macrocycles in Drug Discovery─Learning from the Past for the Future,” Journal of Medicinal Chemistry, 66(8), pp. 5377–5396. Available at: https://doi.org/10.1021/acs.jmedchem.3c00134.
- FreeForm Theory. https://docs.eyesopen.com/applications/szybki/theory/freeform_theory.html
- FreeForm–构象稳定性评估及其在先导化合物优化中的应用. http://blog.molcalx.com.cn/2016/07/02/freeform-conformer-stability.html
- 用计算方法研究大环分子的构象预组织——BCL6抑制剂的案例分析. http://blog.molcalx.com.cn/2024/05/06/bcl6-inhibitor-macrocylization.html
- 用计算构象预组织对大环CDK2抑制剂设计进行优先级排序. http://blog.molcalx.com.cn/2024/05/14/prioritizing-macrocyclic-cdk2-inhibitors.html
- Foloppe, N. and Chen, I.J. (2016) “Towards understanding the unbound state of drug compounds: Implications for the intramolecular reorganization energy upon binding,” Bioorganic and Medicinal Chemistry, 24(10), pp. 2159–2189. Available at: https://doi.org/10.1016/j.bmc.2016.03.022.
- Boström, J., Norrby, P.O. and Liljefors, T. (1998) “Conformational energy penalties of protein-bound ligands.,” Journal of computer-aided molecular design, 12(4), pp. 383–96. Available at: https://doi.org/10.1023/a:1008007507641.
- Perola, E. and Charifson, P.S. (2004) “Conformational Analysis of Drug-Like Molecules Bound to Proteins: An Extensive Study of Ligand Reorganization upon Binding,” Journal of Medicinal Chemistry, 47(10), pp. 2499–2510. Available at: https://doi.org/10.1021/jm030563w.
- Johnson, T.W. et al. (2014) “Discovery of (10 R)-7-Amino-12-fluoro-2,10,16-trimethyl-15-oxo-10,15,16,17- tetrahydro- 2H -8,4-(metheno)pyrazolo[4,3- h ][2,5,11]- benzoxadiazacyclotetradecine-3-carbonitrile (PF-06463922), a macrocyclic inhibitor of anaplastic lymphoma kinase (ALK) and c-ros oncogene 1 (ROS1) with preclinical brain exposure and broad-spectrum potency against ALK-resistant mutations,” Journal of Medicinal Chemistry, 57(11), pp. 4720–4744. Available at: https://doi.org/10.1021/jm500261q.
- Wagner, V. et al. (2017) “Computational Macrocyclization: From de novo Macrocycle Generation to Binding Affinity Estimation,” ChemMedChem, 12(22), pp. 1866–1872. Available at: https://doi.org/10.1002/cmdc.201700478.
- Udvarhelyi, A., Rodde, S. & Wilcken, R. ReSCoSS: a flexible quantum chemistry workflow identifying relevant solution conformers of drug-like molecules. J Comput Aided Mol Des. 2021,35,399–415. https://doi.org/10.1007/s10822-020-00337-7
- Flare V8.0. http://www.cresset-group.com/software/flare
- xTB Version 6.7.0. Semiempirical Extended Tight-Binding Program Package. https://github.com/grimme-lab/xtb
- Bannwarth, C. et al. (2021) “Extended tight-binding quantum chemistry methods,” Wiley Interdisciplinary Reviews: Computational Molecular Science. Blackwell Publishing Inc. Available at: https://doi.org/10.1002/wcms.1493.
- Grimme, S. et al. (2021) “R2SCAN-3c: A ‘swiss army knife’ composite electronic-structure method,” Journal of Chemical Physics, 154(6). Available at: https://doi.org/10.1063/5.0040021.
- Spicher, S. and Grimme, S. (2021) “Single-Point Hessian Calculations for Improved Vibrational Frequencies and Rigid-Rotor-Harmonic-Oscillator Thermodynamics,” Journal of Chemical Theory and Computation, 17(3), pp. 1701–1714. Available at: https://doi.org/10.1021/acs.jctc.0c01306.
联系我们、获取试用或商务合作
想要亲自计算或在自己的项目中使用Flare,或者商务合作,请联系我们。



