摘要:本教程介绍了核磁共振谱图的相关概念,并以丁烷分子为例,详细介绍了如何利用Gaussian程序计算可与实验测量值直接比较的化学位移与耦合常数。
作者:陈宇
日期:2018-06-19
1. 基本概念
1.1 自旋量子数(spin quantum number)
自旋量子数是原子核的基本特征,由原子序数和原子质量共同决定,表1给出了计算给定原子核自旋量子数的一般规则:
Table 1. 原子核的自旋量子数
| I | 原子质量 | 原子序数 | 原子核例子 |
|---|---|---|---|
| 半整数 | 奇数 | 奇数 | 1H(1/2), 3H(1/2) |
| 半整数 | 奇数 | 偶数 | 13C(1/2), 17O(1/2) |
| 整数 | 偶数 | 奇数 | 2H(1), 14N(1) |
| 零 | 偶数 | 偶数 | 12C(0) |
例如1H(1/2),表示原子质量为1,原子序数为1的氢原子核自旋量子数为1/2。
原子核带正电荷,但对于自旋量子数为0的原子核,不会产生磁场;而对于自旋不为0的原子核,其自旋能够产生环绕电流,进而产生磁矩(这也是能够生成核磁共振谱图的基础)。
1.2 核磁共振谱(NMR)
核磁共振谱可以认为是一种吸收光谱,在一定的磁场条件下,具有非0自旋量子数的原子核能够产生能级裂分,进而能够吸收特定波段的电磁辐射,由此得到的吸收峰频率对吸收峰强度的谱图即为核磁共振谱图。
对于自旋量子数为I=1/2的原子核,由于其电荷具有均匀的球形分布,因而这些核磁谱图也最容易获得,这其中最常用的就是1H-NMR和13C-NMR。
1.3 磁屏蔽效应(Magnetic shielding effect)
由于原子核被电子云包围,同时电子云密度又随着不同的化学环境而变化,这种电子云密度变化引起的原子核实际吸收频率的改变是利用核磁共振区分处于不同化学环境下原子核的基础。这种原子核外电子云密度的改变对原子核吸收频率的影响也称为磁屏蔽效应。
1.4 化学位移(chemical shift)
由于磁屏蔽效应的存在,使得在一定的外加磁场强度下,不同化学环境下的相同原子核的吸收频率有所不同,这种吸收频率的改变也称为化学位移。
1.5 自旋偶合(spin coupling)
分子中的质子会产生自旋,而邻近的质子之间会产生相互作用,从而影响对方的核磁共振吸收,这种相互作用称为自旋偶合。而自旋偶合的度量称为偶合常数(在核磁谱图上表现为峰裂距)。
2.利用Gaussian程序计算NMR谱图
Gaussian程序提供了NMR关键字计算磁屏蔽张量,但是实际得到的磁屏蔽值并不能与实验值直接对比,而是需要再计算一个实际实验中选为参比物的分子,两个分子中相同原子核的计算磁屏蔽值相减,即可得到可与实验值直接对比的化学位移值。通常在实验中会选用TMS(四甲基硅烷)作为参比物,在我们的例子中,也选用TMS作为参比物。并计算乙烷的1H和13C的化学位移值。
计算NMR的基本流程:
- 结构优化
- 样品分子与参比分子的NMR计算
- 样品分子的化学位移计算
首先优化需要计算NMR的分子,得到分子最稳定的构象,方法基组可以不必与计算NMR的方法基组一致。
使用优化好的分子作为初始结构,进行NMR的计算,通常要使用更大的基组。这一步计算获得样品分子的磁屏蔽值。
用参比物中H和C的磁屏蔽值分别减去样品分子中同种原子核的磁屏蔽值,即可获得与实验测量值相对照的化学位移值。
需要注意的是:
- 计算参比物分子与计算样品分子必须使用相同的方法和基组;
- 如果分子有多种构象,并且其能量与最稳定构象能量接近,则磁屏蔽值需要取加权平均值。请参照ECD计算与VCD计算教程,详述了如何用多个构象计算CD图谱,NMR图谱与此类似。
在这个教程中,我们以丁烷分子为例,由于其存在两种构象,我们以此演示如何对最终结果进行加权平均计算。
3. 操作步骤
3.1 参比分子TMS的磁屏蔽张量计算
3.1.1 TMS的结构优化
TMS结构优化的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #p opt freq apfd/6-311+g(2d,p) TMS-Opt at APFD/6-311+g(2d,p) level 0 1 Si -2.59493665 -0.23734177 0.00000000 C -1.94825879 0.67717458 1.58400366 H -0.87825881 0.67699200 1.58410113 H -2.30475384 1.68604090 1.58390608 H -2.30509104 0.17288877 2.45765495 C -1.94829217 -2.06639916 0.00000000 H -2.30494861 -2.57079155 0.87366155 H -2.30498142 -2.57080315 -0.87364146 H -0.87829217 -2.06641234 -0.00002009 C -4.53493664 -0.23731786 0.00000000 H -4.89159056 0.77149042 0.00195626 H -4.89160919 -0.74002147 -0.87462780 H -4.89160974 -0.74340939 0.87267157 C -1.94825879 0.67717458 -1.58400366 H -2.30498818 1.68595807 -1.58404957 H -0.87825879 0.67724055 -1.58395763 H -2.30485672 0.17272306 -2.45765495 !此行请用空白行代替,不要忽略任何空白行 |
3.1.2 TMS的磁屏蔽张量计算
使用第一步优化得到的结构作为初始结构,计算磁屏蔽张量。在本教程中在apfd/6-311+g(2d,p)理论水平下计算,关键词如下:
1 | #p NMR apfd/6-311+g(2d,p) |
3.1.3 利用GaussView查看原子核的磁屏蔽值
- 用GaussView读入计算结果
- 展示原子磁屏蔽值
- 展示H原子磁屏蔽值
GaussView 6|File|Open: 读入Gaussian的输出文件TMS-NMR.log,结果如图1所示:
图1. 读入计算结果文件
GaussView Results|NMR 在Results下拉菜单中点击NMR选项,显示原子核磁屏蔽值, 如图2所示。
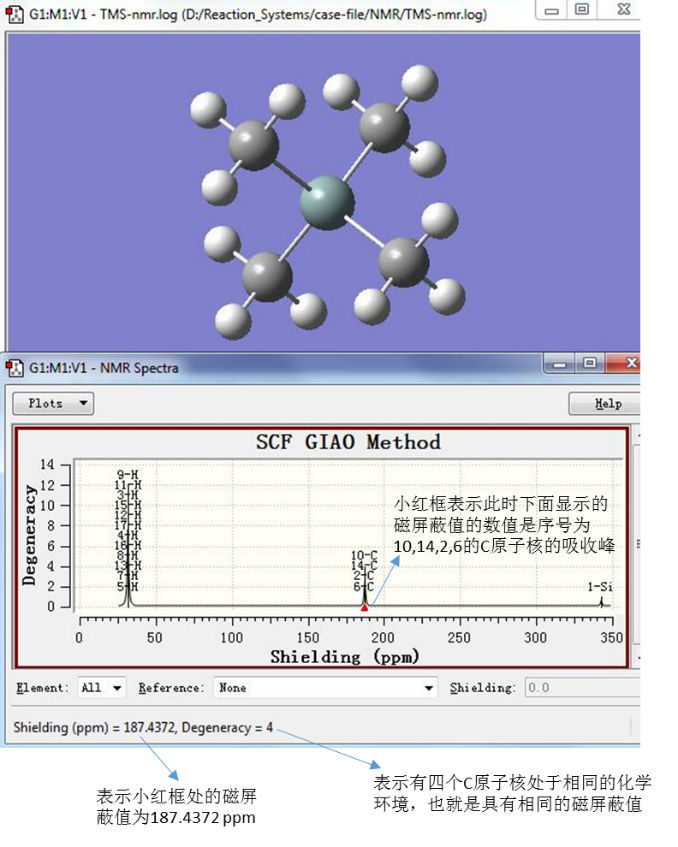
图2. 显示磁屏蔽值
如图2所示,计算结果显示TMS中的四个C原子具有相同的磁屏蔽值187.4372 ppm。
点击图中H吸收峰的位置就可以查看H的磁屏蔽值,结果如图3所示。
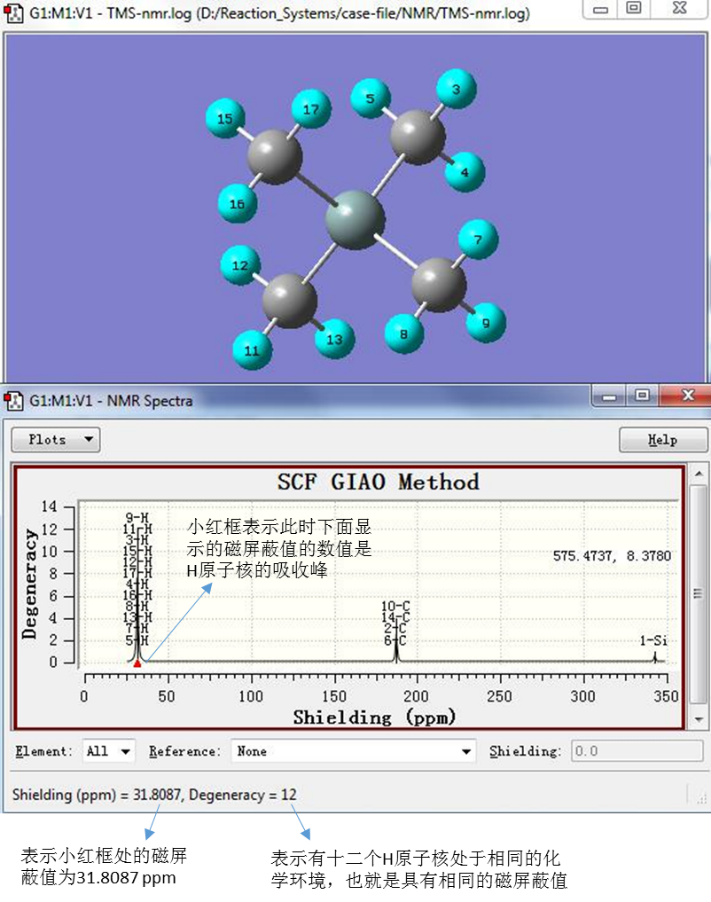
图3. H原子的磁屏蔽值
计算结果显示TMS中的十二个H原子核具有相同的磁屏蔽值31.8087 ppm。
3.2 丁烷的磁屏蔽张量计算
步骤与计算TMS磁屏蔽张量完全一致,区别在于丁烷是个柔性分子,具有多个低能构象(具体的构象搜索见CONFLEX教程 | 构象搜索),每个低能构象都需要分别进行磁屏蔽张量计算。正丁烷的两个构象如下图4所示:
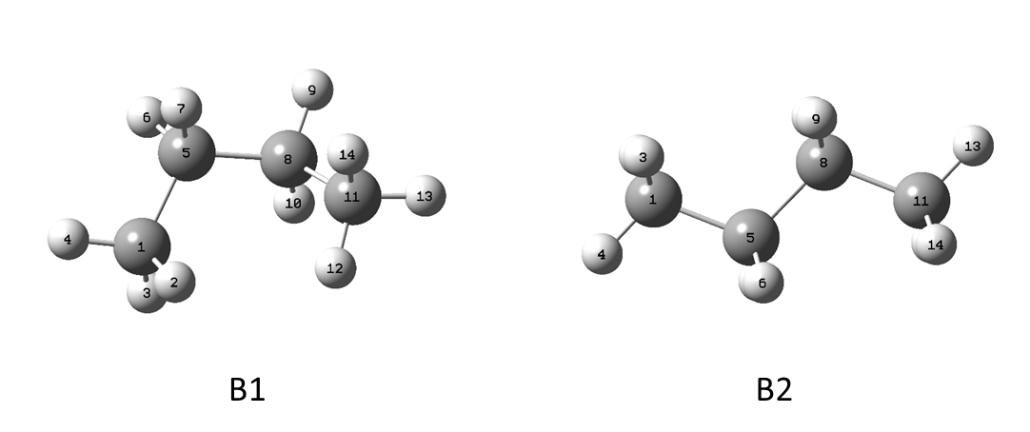
图4. 正丁烷的两个构象
3.2.1 丁烷的结构优化
丁烷的B1构象结构优化输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | # opt freq APFD/6-311+g(2d,p) B1 0 1 C 0.00000000 0.00000000 0.00000000 H 1.09390000 0.00000000 0.00000000 H -0.34680000 -0.52330000 0.89660000 H -0.33130000 1.04140000 0.06630000 C -0.55760000 -0.64560000 -1.25920000 H -1.64660000 -0.51780000 -1.26370000 H -0.17290000 -0.11820000 -2.13990000 C -0.24380000 -2.13810000 -1.36790000 H -0.77020000 -2.54150000 -2.24120000 H -0.63440000 -2.66650000 -0.49050000 C 1.24020000 -2.43530000 -1.51770000 H 1.79830000 -2.15340000 -0.62000000 H 1.39390000 -3.50690000 -1.68040000 H 1.66420000 -1.89880000 -2.37240000 !此行请用空白行代替,不要忽略任何空白行 |
从计算结果可以发现优化过后丁烷的B1构象自由能为-158.259440 Hartree:
1 2 3 4 5 6 7 8 | Zero-point correction= 0.132096 (Hartree/Particle) Thermal correction to Energy= 0.137801 Thermal correction to Enthalpy= 0.138745 Thermal correction to Gibbs Free Energy= 0.104065 Sum of electronic and zero-point Energies= -158.231409 Sum of electronic and thermal Energies= -158.225704 Sum of electronic and thermal Enthalpies= -158.224760 Sum of electronic and thermal Free Energies= -158.259440 |
丁烷的B2构象结构优化输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | # opt freq APFD/6-311+g(2d,p) B2 0 1 C 0.00000000 0.00000000 0.00000000 H 1.09470000 0.00000000 0.00000000 H -0.34390000 0.48080000 -0.92140000 H -0.33970000 -1.04040000 -0.01250000 C -0.54490000 0.71710000 1.22490000 H -1.64010000 0.67090000 1.21120000 H -0.20960000 0.19280000 2.12740000 C -0.08730000 2.17360000 1.27040000 H -0.42260000 2.69780000 0.36790000 H 1.00790000 2.21970000 1.28410000 C -0.63220000 2.89060000 2.49530000 H -0.28820000 2.40990000 3.41670000 H -0.29250000 3.93100000 2.50780000 H -1.72680000 2.89060000 2.49530000 !此行请用空白行代替,不要忽略任何空白行 |
从计算结果可以发现优化过后丁烷的B2构象自由能为-158.260506 Hartree:
1 2 3 4 5 6 7 8 | Zero-point correction= 0.131984 (Hartree/Particle) Thermal correction to Energy= 0.137727 Thermal correction to Enthalpy= 0.138671 Thermal correction to Gibbs Free Energy= 0.104025 Sum of electronic and zero-point Energies= -158.232547 Sum of electronic and thermal Energies= -158.226805 Sum of electronic and thermal Enthalpies= -158.225860 Sum of electronic and thermal Free Energies= -158.260506 |
3.2.2 丁烷的磁屏蔽张量计算
使用第一步优化得到的结构作为初始结构,计算磁屏蔽张量。
丁烷的B1构象的磁屏蔽张量计算输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | # APFD/6-311+g(2d,p) NMR B1-NMR 0 1 C -1.56634800 -0.55470700 -0.12464800 H -1.14865200 -1.51160600 0.19876800 H -1.66239900 -0.58932300 -1.21475600 H -2.57392900 -0.48267600 0.29368600 C -0.69844800 0.62141300 0.31008400 H -1.20473900 1.55761600 0.04706400 H -0.60582900 0.62574900 1.40379100 C 0.69844700 0.62141300 -0.31008400 H 1.20473900 1.55761600 -0.04706300 H 0.60582900 0.62574800 -1.40379100 C 1.56634900 -0.55470700 0.12464800 H 1.14865600 -1.51160500 -0.19877500 H 2.57393200 -0.48267100 -0.29367900 H 1.66239200 -0.58932700 1.21475700 !此行请用空白行代替,不要忽略任何空白行 |
除了用3.1.3所述的GaussView查看磁屏蔽张量外,还可以直接从Gaussian的输出文件读取,找shielding tensor行就可以了,如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | Calculating GIAO nuclear magnetic shielding tensors. SCF GIAO Magnetic shielding tensor (ppm): 1 C Isotropic = 174.2868 Anisotropy = 21.5592 XX= 173.7926 YX= 10.6913 ZX= 1.5893 XY= 14.5744 YY= 172.1941 ZY= 5.9818 XZ= 1.2229 YZ= 7.9728 ZZ= 176.8738 Eigenvalues: 159.2918 174.9090 188.6596 2 H Isotropic = 30.6727 Anisotropy = 7.2805 XX= 30.2473 YX= 0.6980 ZX= 0.7511 XY= -0.3559 YY= 35.1824 ZY= -1.8872 XZ= 0.4308 YZ= -1.6162 ZZ= 26.5883 Eigenvalues: 26.1532 30.3385 35.5263 3 H Isotropic = 31.3010 Anisotropy = 8.9957 XX= 29.9747 YX= 1.6085 ZX= 3.2021 XY= 1.2196 YY= 28.3833 ZY= 2.2118 XZ= 2.6337 YZ= 1.1795 ZZ= 35.5450 Eigenvalues: 27.5564 29.0484 37.2982 4 H Isotropic = 30.7697 Anisotropy = 10.2205 XX= 36.5784 YX= 1.4508 ZX= -2.6033 XY= 2.4589 YY= 27.9164 ZY= 0.0975 XZ= -2.4030 YZ= 0.5372 ZZ= 27.8141 Eigenvalues: 26.5397 28.1860 37.5833 5 C Isotropic = 160.6909 Anisotropy = 16.5837 XX= 170.4320 YX= -5.7462 ZX= -3.7253 XY= 1.4825 YY= 153.3652 ZY= 0.5205 XZ= -3.5183 YZ= 2.1754 ZZ= 158.2755 Eigenvalues: 152.9267 157.3992 171.7467 6 H Isotropic = 30.1633 Anisotropy = 9.1505 XX= 31.1098 YX= -3.3431 ZX= 0.0238 XY= -3.0403 YY= 34.2824 ZY= -0.3294 XZ= -0.1753 YZ= -0.2164 ZZ= 25.0977 Eigenvalues: 25.0837 29.1426 36.2636 7 H Isotropic = 30.6069 Anisotropy = 7.8941 XX= 29.1186 YX= 0.9870 ZX= -0.8250 XY= 0.5761 YY= 27.7261 ZY= 2.8093 XZ= -0.3615 YZ= 2.5348 ZZ= 34.9759 Eigenvalues: 26.5157 29.4354 35.8697 8 C Isotropic = 160.6908 Anisotropy = 16.5837 XX= 170.4319 YX= 5.7463 ZX= -3.7253 XY= -1.4824 YY= 153.3652 ZY= -0.5206 XZ= -3.5184 YZ= -2.1756 ZZ= 158.2754 Eigenvalues: 152.9267 157.3991 171.7466 9 H Isotropic = 30.1633 Anisotropy = 9.1505 XX= 31.1098 YX= 3.3431 ZX= 0.0238 XY= 3.0403 YY= 34.2824 ZY= 0.3294 XZ= -0.1753 YZ= 0.2164 ZZ= 25.0976 Eigenvalues: 25.0836 29.1426 36.2636 10 H Isotropic = 30.6069 Anisotropy = 7.8941 XX= 29.1186 YX= -0.9870 ZX= -0.8250 XY= -0.5761 YY= 27.7262 ZY= -2.8093 XZ= -0.3615 YZ= -2.5348 ZZ= 34.9759 Eigenvalues: 26.5157 29.4354 35.8697 11 C Isotropic = 174.2867 Anisotropy = 21.5593 XX= 173.7925 YX= -10.6913 ZX= 1.5893 XY= -14.5744 YY= 172.1939 ZY= -5.9820 XZ= 1.2229 YZ= -7.9729 ZZ= 176.8737 Eigenvalues: 159.2916 174.9089 188.6596 12 H Isotropic = 30.6726 Anisotropy = 7.2805 XX= 30.2472 YX= -0.6980 ZX= 0.7511 XY= 0.3559 YY= 35.1824 ZY= 1.8873 XZ= 0.4308 YZ= 1.6162 ZZ= 26.5883 Eigenvalues: 26.1532 30.3384 35.5263 13 H Isotropic = 30.7697 Anisotropy = 10.2205 XX= 36.5785 YX= -1.4508 ZX= -2.6032 XY= -2.4589 YY= 27.9164 ZY= -0.0976 XZ= -2.4030 YZ= -0.5372 ZZ= 27.8141 Eigenvalues: 26.5397 28.1860 37.5833 14 H Isotropic = 31.3010 Anisotropy = 8.9957 XX= 29.9747 YX= -1.6085 ZX= 3.2020 XY= -1.2196 YY= 28.3833 ZY= -2.2119 XZ= 2.6337 YZ= -1.1795 ZZ= 35.5450 Eigenvalues: 27.5564 29.0484 37.2981 |
丁烷的B2构象的磁屏蔽张量计算输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | # APFD/6-311+g(2d,p) NMR B2-NMR 0 1 C 1.94683700 0.11896000 0.00000100 H 2.09129900 0.75087700 0.88185300 H 2.09130000 0.75088000 -0.88184900 H 2.73868600 -0.63492600 0.00000000 C 0.56168600 -0.51486300 -0.00000100 H 0.45228200 -1.16761700 -0.87536000 H 0.45228100 -1.16761900 0.87535700 C -0.56168500 0.51486300 -0.00000100 H -0.45228200 1.16761800 -0.87536000 H -0.45228100 1.16761900 0.87535700 C -1.94683700 -0.11895900 0.00000100 H -2.09130100 -0.75087400 0.88185500 H -2.73868600 0.63492600 -0.00000600 H -2.09129800 -0.75088400 -0.88184700 !此行请用空白行代替,不要忽略任何空白行 |
结果如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | Calculating GIAO nuclear magnetic shielding tensors. SCF GIAO Magnetic shielding tensor (ppm): 1 C Isotropic = 171.2758 Anisotropy = 27.1275 XX= 187.4432 YX= 3.3907 ZX= 0.0000 XY= 9.8413 YY= 166.5347 ZY= 0.0000 XZ= 0.0000 YZ= 0.0000 ZZ= 159.8495 Eigenvalues: 159.8495 164.6171 189.3608 2 H Isotropic = 30.9697 Anisotropy = 8.3806 XX= 31.1124 YX= 2.5925 ZX= -2.7644 XY= 1.8252 YY= 29.9448 ZY= -3.7728 XZ= -2.1681 YZ= -3.2829 ZZ= 31.8518 Eigenvalues: 27.2170 29.1353 36.5568 3 H Isotropic = 30.9697 Anisotropy = 8.3806 XX= 31.1124 YX= 2.5925 ZX= 2.7644 XY= 1.8252 YY= 29.9448 ZY= 3.7728 XZ= 2.1681 YZ= 3.2829 ZZ= 31.8518 Eigenvalues: 27.2170 29.1353 36.5567 4 H Isotropic = 30.6632 Anisotropy = 10.2798 XX= 35.8803 YX= -4.2670 ZX= 0.0000 XY= -2.8777 YY= 29.7163 ZY= 0.0000 XZ= 0.0000 YZ= 0.0000 ZZ= 26.3930 Eigenvalues: 26.3930 28.0802 37.5164 5 C Isotropic = 158.0633 Anisotropy = 24.2807 XX= 172.1041 YX= -2.0673 ZX= 0.0000 XY= -10.2328 YY= 156.6285 ZY= 0.0000 XZ= 0.0000 YZ= -0.0001 ZZ= 145.4573 Eigenvalues: 145.4573 154.4822 174.2504 6 H Isotropic = 30.5268 Anisotropy = 6.7494 XX= 30.5065 YX= 0.0523 ZX= -0.2601 XY= 0.4280 YY= 30.9499 ZY= -4.5943 XZ= 0.1212 YZ= -4.3242 ZZ= 30.1238 Eigenvalues: 26.0558 30.4981 35.0263 7 H Isotropic = 30.5268 Anisotropy = 6.7493 XX= 30.5065 YX= 0.0523 ZX= 0.2602 XY= 0.4280 YY= 30.9499 ZY= 4.5943 XZ= -0.1212 YZ= 4.3242 ZZ= 30.1238 Eigenvalues: 26.0558 30.4981 35.0263 8 C Isotropic = 158.0632 Anisotropy = 24.2808 XX= 172.1040 YX= -2.0673 ZX= 0.0000 XY= -10.2328 YY= 156.6285 ZY= 0.0000 XZ= 0.0000 YZ= 0.0000 ZZ= 145.4572 Eigenvalues: 145.4572 154.4821 174.2504 9 H Isotropic = 30.5267 Anisotropy = 6.7494 XX= 30.5065 YX= 0.0523 ZX= 0.2601 XY= 0.4280 YY= 30.9499 ZY= 4.5943 XZ= -0.1212 YZ= 4.3242 ZZ= 30.1238 Eigenvalues: 26.0558 30.4981 35.0263 10 H Isotropic = 30.5268 Anisotropy = 6.7493 XX= 30.5065 YX= 0.0523 ZX= -0.2601 XY= 0.4280 YY= 30.9499 ZY= -4.5943 XZ= 0.1212 YZ= -4.3242 ZZ= 30.1238 Eigenvalues: 26.0558 30.4981 35.0263 11 C Isotropic = 171.2757 Anisotropy = 27.1275 XX= 187.4431 YX= 3.3907 ZX= 0.0000 XY= 9.8414 YY= 166.5346 ZY= 0.0000 XZ= 0.0001 YZ= 0.0000 ZZ= 159.8494 Eigenvalues: 159.8494 164.6170 189.3607 12 H Isotropic = 30.9696 Anisotropy = 8.3806 XX= 31.1124 YX= 2.5925 ZX= 2.7645 XY= 1.8252 YY= 29.9447 ZY= 3.7728 XZ= 2.1682 YZ= 3.2829 ZZ= 31.8518 Eigenvalues: 27.2170 29.1352 36.5567 13 H Isotropic = 30.6632 Anisotropy = 10.2798 XX= 35.8803 YX= -4.2670 ZX= 0.0000 XY= -2.8777 YY= 29.7163 ZY= 0.0000 XZ= 0.0000 YZ= 0.0000 ZZ= 26.3930 Eigenvalues: 26.3930 28.0802 37.5164 14 H Isotropic = 30.9696 Anisotropy = 8.3806 XX= 31.1124 YX= 2.5925 ZX= -2.7644 XY= 1.8252 YY= 29.9448 ZY= -3.7728 XZ= -2.1681 YZ= -3.2829 ZZ= 31.8517 Eigenvalues: 27.2170 29.1352 36.5567 |
3.3 丁烷的碳谱计算
我们以C谱为例,说明如何获得加权平均的磁屏蔽值。
3.3.1 权重计算
首先用每个构象的构象自由能计算不同构象在所有构象中所占的权重P,如表2所示。
Table 2. 构象的玻尔兹曼权重P
| 构象 | G(Hartree) | ΔG(Hartree) | qi | 权重Pi |
|---|---|---|---|---|
| B1 | -158.259440 | 0.001066 | 0.32 | 24% |
| B2 | -158.260506 | 0.0 | 1 | 76% |
其中G为分子自由能,取相对值(ΔG)时,通常将能量最低的构象定为零点,根据平衡常数与自由能变的关系可以得到:
q=e-ΔG/RT
其中R为气体常数(R=8.314472J/mol·K),T为温度,ΔG的能量单位需要换算成kcal/mol)。
构象i出现的概率(Pi)服从玻尔兹曼分布:
Pi = qi/Σqi
我们在下表3中列出了TMS和丁烷的计算磁屏蔽值,在这个例子中,我们以TMS作为参比物,因此将其化学位移定为0,然后分别用TMS中C的计算磁屏蔽值减去乙烷中C的计算磁屏蔽值,从而得到乙烷的化学位移,这个值可以直接与实验测量值相比较(H原子的化学位移值计算方法完全相同)。
Table 3. 丁烷的13C-NMR计算
| 原子编号 | B1(ppm) | B2(ppm) | 加权平均值 | 化学位移值 |
|---|---|---|---|---|
| C1 | 174.2867 | 171.2758 | 171.9984 | 15.4388 |
| C5 | 160.6909 | 158.0633 | 158.6939 | 28.7433 |
| C8 | 160.6909 | 158.0633 | 158.6939 | 28.7433 |
| C11 | 174.2867 | 171.2758 | 171.9984 | 15.4388 |
| TMS 13C (ppm) | 187.4372 | |||
对于某个原子,加权平均值等于这个原子在每个构象中磁屏蔽值与此构象权重之积的加和。例如对于C1,加权平均值 = 174.2867*24% + 171.2758*76% = 171.9984 ppm 。
3.4 耦合常数的计算
由于相互作用的核之间的偶合常数是分子的固有性质,因此通过计算偶合常数对确定分子的结构具有重要的意义。Gaussian能够计算自旋核之间的偶合常数,我们以B2构象为例计算其偶合常数。
计算构象B2偶合常数的输入文件:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | # APFD/6-311+g(2d,p) NMR=spinspin B2-coupling constant 0 1 C 1.94683700 0.11896000 0.00000100 H 2.09129900 0.75087700 0.88185300 H 2.09130000 0.75088000 -0.88184900 H 2.73868600 -0.63492600 0.00000000 C 0.56168600 -0.51486300 -0.00000100 H 0.45228200 -1.16761700 -0.87536000 H 0.45228100 -1.16761900 0.87535700 C -0.56168500 0.51486300 -0.00000100 H -0.45228200 1.16761800 -0.87536000 H -0.45228100 1.16761900 0.87535700 C -1.94683700 -0.11895900 0.00000100 H -2.09130100 -0.75087400 0.88185500 H -2.73868600 0.63492600 -0.00000600 H -2.09129800 -0.75088400 -0.88184700 !此行请用空白行代替,不要忽略任何空白行 |
计算完毕,用文本形式打开生成的log文件,找到” Total nuclear spin-spin coupling J (Hz):”行,发现如下的内容:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | Total nuclear spin-spin coupling J (Hz): 1 2 3 4 5 1 0.000000D+00 2 0.110557D+03 0.000000D+00 3 0.110557D+03 -0.128264D+02 0.000000D+00 4 0.111188D+03 -0.132128D+02 -0.132128D+02 0.000000D+00 5 0.314828D+02 -0.425964D+01 -0.425964D+01 -0.336114D+01 0.000000D+00 6 -0.381208D+01 0.125633D+02 0.362258D+01 0.311607D+01 0.111576D+03 7 -0.381209D+01 0.362260D+01 0.125633D+02 0.311606D+01 0.111575D+03 8 -0.702696D+00 0.251103D+01 0.251104D+01 0.108429D+02 0.315786D+02 9 0.232266D+01 -0.360124D+00 -0.142846D+00 -0.549483D+00 -0.402395D+01 10 0.232270D+01 -0.142845D+00 -0.360123D+00 -0.549477D+00 -0.402396D+01 11 0.596981D+01 -0.353717D+00 -0.353717D+00 0.919497D+00 -0.702699D+00 12 -0.353719D+00 -0.422193D-01 -0.510821D-01 -0.211258D+00 0.251097D+01 13 0.919491D+00 -0.211257D+00 -0.211258D+00 0.793923D-03 0.108428D+02 14 -0.353717D+00 -0.510849D-01 -0.422229D-01 -0.211258D+00 0.251107D+01 6 7 8 9 10 6 0.000000D+00 7 -0.132970D+02 0.000000D+00 8 -0.402399D+01 -0.402399D+01 0.000000D+00 9 0.372224D+01 0.110580D+02 0.111576D+03 0.000000D+00 10 0.110580D+02 0.372220D+01 0.111575D+03 -0.132971D+02 0.000000D+00 11 0.232266D+01 0.232269D+01 0.314828D+02 -0.381209D+01 -0.381211D+01 12 -0.360124D+00 -0.142845D+00 -0.425962D+01 0.125633D+02 0.362265D+01 13 -0.549482D+00 -0.549476D+00 -0.336109D+01 0.311610D+01 0.311600D+01 14 -0.142845D+00 -0.360122D+00 -0.425965D+01 0.362254D+01 0.125633D+02 11 12 13 14 11 0.000000D+00 12 0.110557D+03 0.000000D+00 13 0.111188D+03 -0.132127D+02 0.000000D+00 14 0.110556D+03 -0.128264D+02 -0.132128D+02 0.000000D+00 |
其中行和列的1到14为原子编号,而矩阵中对应的数值则为相应两个原子核间的偶合常数,例如1和2号原子的偶合常数为110.557 Hz。
4. 参考文献
- Exploring Chemistry with Electronic Structure Methods, 3rd ed., Gaussian, Inc.: Wallingford, CT, 2015. J. B. Foresman and Æ Frisch
- Gaussian使用手册NMR关键词:http://gaussian.com/nmr
本书的第161-170页《Predicting Spectra: NMR》详细地介绍了如何用Gaussian计算NMR,并进行玻尔兹曼加权平均获得最终的NMR图谱。
5. 相关资料
- 构象搜索
- 红外与VCD图谱计算
- 紫外与ECD图谱计算
- DP4-AI自动NMR数据分析:直接从光谱到结构
柔性化合物的光谱是多个低能构象的光谱的玻尔兹曼加权平均图谱,因此需要对化合物进行构象搜索,我们提供至少3种不同软件的构象搜索方法:(1) CONFLEX教程 | 构象搜索;(2)Torch教程–构象搜索;(3)GMMX构像搜索(见GaussView自带教程)。
《Gaussian教程 | VCD计算》详述了如何从构象搜索开始计算化合物的VCD图谱,同时也得到IR图谱。
《Gaussian教程–ECD计算》详述了如何从构象搜索开始计算化合物的ECD图谱,同时也得到UV图谱。
6. 联系我们
Guassian软件采购、获取报价,请联系我们:



