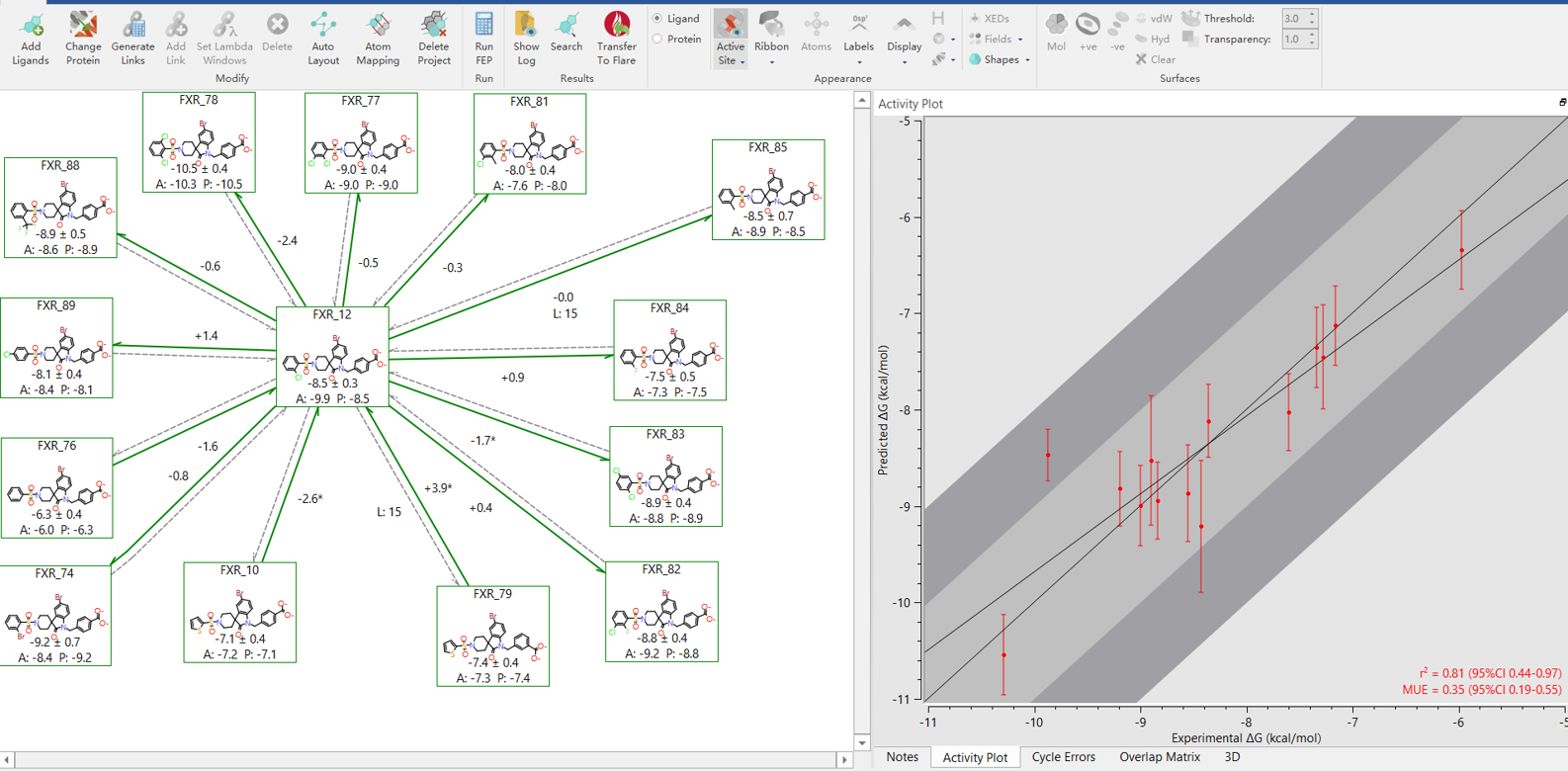
摘要:本文以D3R CG2的Free Energy Set 2数据集的14个IC50跨度为1000倍的FXR激动剂为例,分析了Flare/FEP预测结合亲和力的性能。结果表明,预测值与实验值具有极其显著的相关性:Kendall Tau=0.64, Pearson R=0.90; MUE=0.35;RMSD=0.35。预测值可以显而易见地将高活性化合物与低活性化合物区分为两类。此外,借助云计算资源,整个计算可以在1个小时左右完成。这说明,借助云计算取之不尽的资源,FEP可以帮助药化/计算团队快速、可靠地对结构相似的同系物进行排序,从而加速项目的进度。
肖高铿/2020-07-27
背景
在药物研发过程中,常需对活性分子的特定片段或整体骨架进行结构修饰,以改善其药理学特性(如活性、选择性、ADME性质)或拓展至新颖的化学空间。在苗头化合物(hit)或先导化合物(lead)优化阶段,药物化学研究人员通常借助经典生物等排体替换策略,或利用如SPARK等计算工具,高效生成一系列侧链或骨架替换的候选分子。然而,面对众多结构变体,如何优先选择合成目标成为关键挑战。本文以D3R Grand Challenge 2(GC2)中一组活性差异达三个数量级(IC50 跨越约1000倍)的Farnesoid X受体(FXR)激动剂同系物为模型体系,演示如何利用FLARE FEP方法对候选分子进行高精度排序,以辅助药物化学决策。
FXR激动剂算例介绍
非酒精性脂肪性肝炎(NASH)是一种尚未被充分满足临床需求的疾病,FXR作为其关键治疗靶点,备受关注。D3R Grand Challenge 2(2016–2017)第二阶段的Free Energy Set 2数据集[1]包含18个结构高度相似的FXR激动剂同系物,共享同一母核骨架,但IC50值跨越近三个数量级(约28 nM至41,800 nM),是验证相对结合自由能预测方法的理想基准数据集。D3R GC2采用Kendall’s tau相关系数与中心化均方根误差(RMSEc,单位:kcal/mol)作为主要评价指标。
Schindler等人[2]采用Schrödinger FEP+对这18个化合物进行了相对结合自由能预测。从净电荷分析,其中14个化合物为羧酸根形式(带一个负电荷),其余4个为中性分子。为满足FEP方法对体系电荷一致性的要求,作者在对接过程中将羧基统一处理为中性。计算结果如图1所示,FEP+预测值与实验ΔG具有良好的排序能力:Kendall’s tau = 0.50 ± 0.12,Pearson相关系数R2 = 0.80 ± 0.08,RMSE = 1.31 kcal/mol。相比之下,Prime MM-GBSA方法的性能显著较差(R2 = 0.72 ± 0.11,RMSE = 9.31 kcal/mol)。值得注意的是,即使仅针对14个带电羧酸分子进行FEP+分析,RMSE也仅微降至1.21 kcal/mol,表明电荷一致性处理对整体性能影响有限。
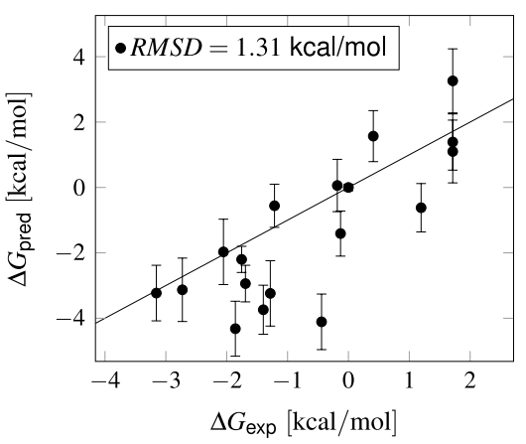
图1. Schindler等人对18个FXR激动剂的ΔG预测结果
数据准备
用Flare下载FXR_12与FXR的复合物结构(PDB 5Q0W),并在默认条件下(pH=7.0)准备蛋白结构,并将配体FXR_12从蛋白中提取分离。其它的化合物以FXR_12为模板,在结合位点里用Flare的结构编辑器直接修改、能量最小化后保存。
鉴于FEP方法不能同时处理不同电荷的分子,本文仅以D3R CG2的Free Energy Set 2数据集中的FXR激动剂的14个带负电荷的羧酸分子(见Table 1)为研究对象,考察FLARE/FEP的预测性能。
准备好的蛋白结构:5Q0W_protein.pdb
准备好的配体结构(带FEP预测结果):fxr-agonist.sdf
准备好用于FEP计算的Flare项目文件(已经包含一个计算结果):D3R-FXR-FEP.flr
Table 1. 14个FXR激动剂的结构、IC50(nM)及其预测的ΔG (kcal/mol)
| Structure | ID | IC50(nM) | ΔG(Exp) | ΔG(Pred) |
|
|
FXR_10 | 5640 | -7.2 | -7.1 |
|
|
FXR_12 | 58 | -9.9 | -8.5 |
|
|
FXR_74 | 655 | -8.4 | -9.2 |
|
|
FXR_76 | 41800 | -6.0 | -6.3 |
|
|
FXR_77 | 250 | -9.0 | -9.0 |
|
|
FXR_78 | 28.3 | -10.3 | -10.5 |
|
|
FXR_79 | 4150 | -7.3 | -7.4 |
|
|
FXR_81 | 2690 | -7.6 | -8.0 |
|
|
FXR_82 | 180 | -9.2 | -8.8 |
|
|
FXR_83 | 330 | -8.8 | -8.9 |
|
|
FXR_84 | 4540 | -7.3 | -7.5 |
|
|
FXR_85 | 297 | -8.9 | -8.5 |
|
|
FXR_88 | 540 | -8.6 | -8.9 |
|
|
FXR_89 | 735 | -8.4 | -8.1 |
FEP计算
详细的操作流程请参见:云计算教程 | 用FLARE FEP计算相对结合自由能[3]。这里仅对关键的参数进行描述,如果没有说明则为默认参数。
图的生成
FLARE的FEP计算支持两种类型的图:normal与Star图。Normal图模式精度高,也更耗计算资源;Star图适合于研究结构与活性关系研究,但精度有所损失。本文采用以FXR_12为中心的Star图模式(见Figure 2)。实际上,FXR_16比FXR_12更适合做为Star图的中心分子,因为FXR_16与磺酰基连接的末端芳环为苯环,更加容易转化为其它取代苯环或噻唑环,也就更容易计算成功。
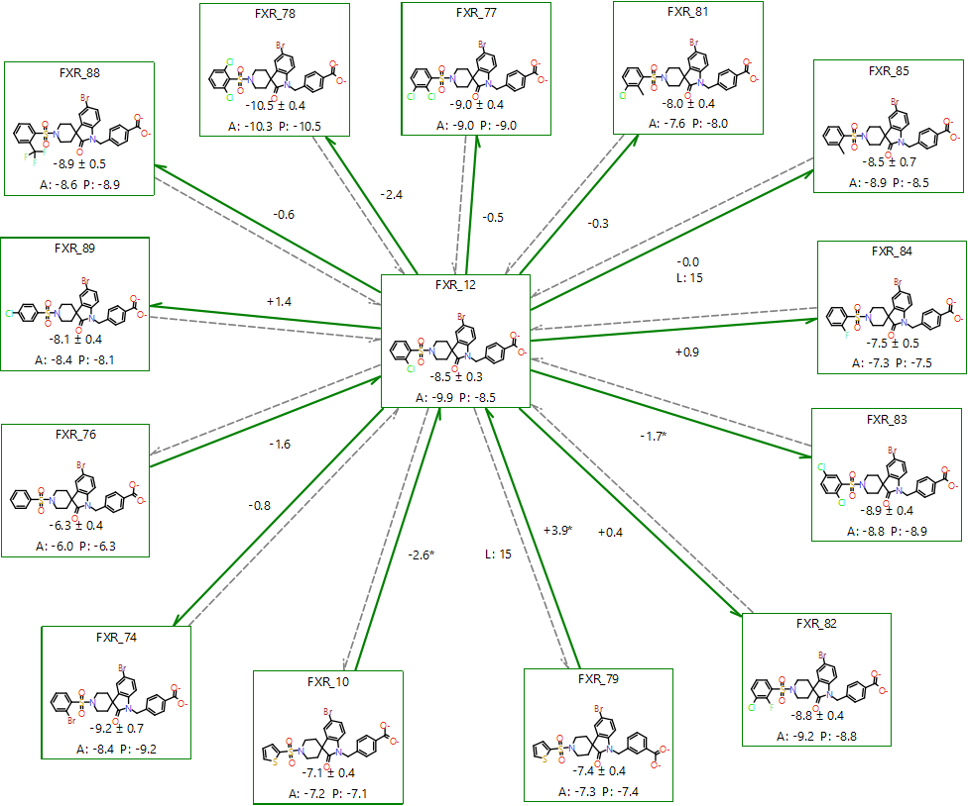
Figure 2. 以FXR_12为中心的星型、单向网络
由于涉及到的14个分子IC50已知,本计算实验的主要目的时考察预测值与实验值的关系,因此生成图的时候采用了Benchmark模式,而不是Product模式。
FEP计算参数
FEP计算时小分子力场采用AMBER/GAFF2,并分配AM1-BCC电荷;体系设置10Å的溶剂盒子;每个体系进行了4 ns的分子动力学模拟;Figure 2中每对分子之间的link采用单向模式(quick mode):每个方向上仅计算从小分子\(→\)大分子的转化,每个方向默认计算9个λ窗口。鉴于FXR_12\(→\)FXR_79有较大的结构变化,因此设置15个λ窗口;FXR_12\(→\)FXR_85也设置了15个λ窗口。
硬件资源:云计算加速FEP计算
如Figure 2所示,共有13个Link,总共有111(9*9+2*15)个λ窗口需要计算,因此至少可以使用111个GPU进行加速计算。在本实验中,采用深圳云端软件公司(Cloudam)的云E算力平台的计算资源进行计算,broker设置最大使用200张GPU,每节点1张Tesla T4卡+4个CPU核心+8GB的内存。
具体的云计算资源使用方法见:云计算教程 | 用FLARE FEP计算相对结合自由能[3]
结果
关于预测性能
ΔG的实验值与预测值见Table 1, Kendall τ与Pearson R相关性系数分别为0.64(p-value=0.001)与0.90(p-value=0.0000145),这表明实验值与预测值之间具有极其显著的相关性;MUE为0.35;RMSD为0.50,比Schindler等人[2]报道的FEP+预测结果RMSD=1.31要低0.8,具有更好的精密度。
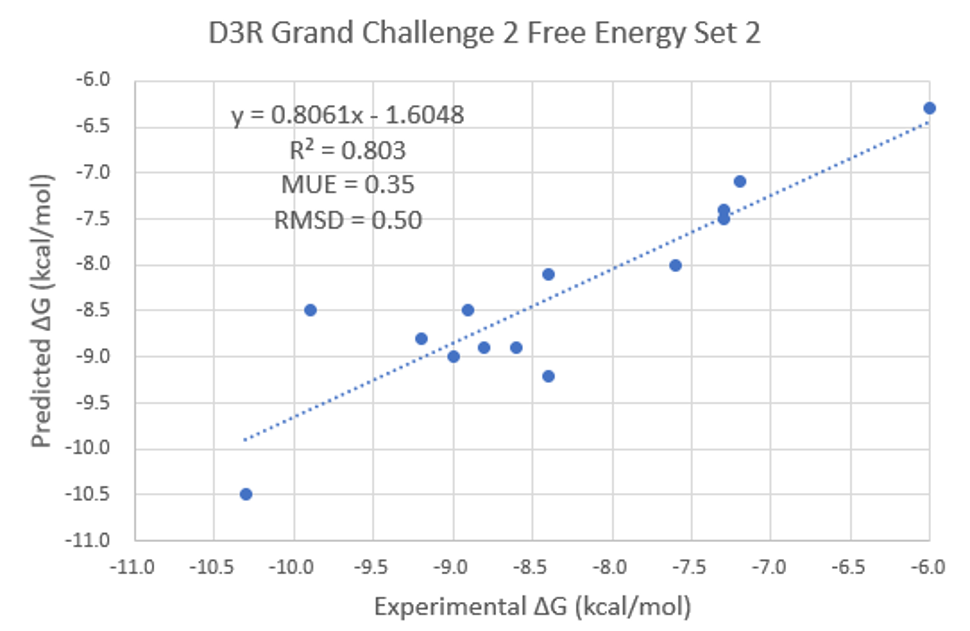
Figure 3. 结合自由能ΔG的实验值与预测值比较
根据Figure 3的ΔG实验值与预测值散点图可以直观地将结合亲和力高、低的化合物聚类区分开:ΔG大于-8.0与小于-8.0的化合物被明显地区分。尤其是IC50大于1000nM的化合物都被被归属于ΔG大的化合物,而IC50最低的几个化合物都聚集在ΔG预测值最小的化合物里。这说明使用Flare/FEP可以帮助药化工作人员可靠地做出化合物排序决策。
更重要的是,几个不同的生物等排体得到很好的排序,尤其是卤素取代苯环的衍生物的排序:1)苯环被噻吩取代对活性不利;2)苯环的氟取代对活性不利;苯环的氯、溴取代对活性有利。这是药物化学研究阶段非常重要的信息,而Flare/FEP可以准确在实验前的告诉你。FEP似乎对低活性化合物识别的特别好:预测为活性最差的5个化合物,确实也对应为IC50最高的5个化合物;在预测活性最高的5个化合物里,包含了实际活性最强的化合物FXR_78。
与不用FEP的方法比较:logP、分子量与打分函数
用Flare计算的SlogP与分子量通常做为空模型,分析SlogP、分子量与实验结合自由能(pIC50)的关系;同时,也用Ligandscout的Binding Affinity Score来预测结合亲和力,分析预测值与实验结合自由能(pIC50)的关系。好的FEP方法,应该要优于空模型与打分函数。结果表明,SlogP、分子量、结合亲和力打分值与pIC50具有强相关性,Pearson相关性系数分别为0.717、0.644与-0.701,远低于Flare FEP的0.9,这说明使用更贵的FEP计算是有价值的,更多的统计学指标见表2。
表2. 结合自由能(pIC50)与logP、分子量、打分函数相关性分析的统计学结果
| Iterms | SlogP | MW | Binding Affinity Score |
| Pearson Correlation (r) | 0.717 | 0.644 | -0.701 |
| Spearman Rank Correlation(ρ) | 0.713 | 0.626 | -0.7 |
| Root Mean Squared Deviation (RMSD) | 1.07 | 589.438 | 54.99 |
与pyAutoFEP比较
在2021年的时候,Carvalho等人发表了自动相对结合自由能计算工作流pyAutoFEP[4],刚好与本文采用了同样的测试集,除了化合物FXR_10之外。在pyAutoFEP测试中,使用AMBER03/GAFF/AM1-BCC without REST2时性能表现最佳:Pearson Correlation r=0.71;RMSE=1.07 kcal/mol。这个预测精度与不用模型的SlogP差不多,这说明了:在这个例子里,使用pyAutoFEP没有比空模型SlogP更好,也就是用了pyAutoFEP没有比不用更好。
关于机时与费用
本实验在Cloudam上计算完成,Cloudam提供了多种GPU型号可供选择,本次计算实验采用价格最低的Tesla T4进行计算。峰值时Flare调用120多张卡,全部计算实验大约在1.15小时内完成,总共机时费大约600元。这说明,此类FEP计算可以在非常合理地时间内完成,为计算和药化团队提供快速、可靠的结果对化合物进行排序与决策。云计算近乎取之不尽的资源为高精度的FEP计算提供了算力保障,真正地加速了项目研发进度。同时,在本计算中,每个化合物的平均计算费用约为42元,略低于之前[3]预计的费用。
相关性系数与RMSD计算
Kendall Tau相关性系数计算
1 2 3 4 5 | import scipy.stats as stats exp = [-7.2,-9.9,-8.4,-6.0,-9.0,-10.3,-7.3,-7.6,-9.2,-8.8,-7.3,-8.9,-8.6,-8.4] pred = [-7.1,-8.5,-9.2,-6.3,-9.0,-10.5,-7.4,-8.0,-8.8,-8.9,-7.5,-8.5,-8.9,-8.1] tau, p_value = stats.kendalltau(exp, pred) print(tau,p_value) |
1 | 0.6404494382022472 0.0016945408238685901 |
Pearson相关性系数R的计算
1 2 3 4 5 | import scipy.stats as stats exp = [-7.2,-9.9,-8.4,-6.0,-9.0,-10.3,-7.3,-7.6,-9.2,-8.8,-7.3,-8.9,-8.6,-8.4] pred = [-7.1,-8.5,-9.2,-6.3,-9.0,-10.5,-7.4,-8.0,-8.8,-8.9,-7.5,-8.5,-8.9,-8.1] r, p_value = stats.pearsonr(exp, pred) print(r,p_value) |
1 | 0.8960225522291245 1.4532438595517099e-05 |
spearman相关性系数R的计算
1 2 3 4 5 | import scipy.stats as stats exp = [-7.2,-9.9,-8.4,-6.0,-9.0,-10.3,-7.3,-7.6,-9.2,-8.8,-7.3,-8.9,-8.6,-8.4] pred = [-7.1,-8.5,-9.2,-6.3,-9.0,-10.5,-7.4,-8.0,-8.8,-8.9,-7.5,-8.5,-8.9,-8.1] rho, p_value = stats.spearmanr(exp, pred) print(rho,p_value) |
1 | 0.7836644591611479 0.000911883738030973 |
ΔG实验值与预测值的RMSD计算
1 2 3 4 5 6 | from sklearn.metrics import mean_squared_error exp = [-7.2,-9.9,-8.4,-6.0,-9.0,-10.3,-7.3,-7.6,-9.2,-8.8,-7.3,-8.9,-8.6,-8.4] pred = [-7.1,-8.5,-9.2,-6.3,-9.0,-10.5,-7.4,-8.0,-8.8,-8.9,-7.5,-8.5,-8.9,-8.1] mse = mean_squared_error(exp, pred) rmse = mse**0.5 print(mse,rmse) |
1 | 0.24714285714285705 0.4971346468944375 |
ΔG实验值与预测值的决策系数R2
1 2 3 4 5 | from sklearn.metrics import r2_score exp = [-7.2,-9.9,-8.4,-6.0,-9.0,-10.3,-7.3,-7.6,-9.2,-8.8,-7.3,-8.9,-8.6,-8.4] pred = [-7.1,-8.5,-9.2,-6.3,-9.0,-10.5,-7.4,-8.0,-8.8,-8.9,-7.5,-8.5,-8.9,-8.1] r2 = r2_score(exp, pred) print(r2) |
1 | 0.8026803535785574 |
FEP预测的MUE计算
FEP的MUE取自Flare/FEP,如下图4所示。
Figure 4. FEP计算完毕的网络图与活性的实验值与预测值比较
文献
- D3R GC2. Drug Design Data Resource. https://drugdesigndata.org/about/grand-challenge-2
- Schindler, C.; Rippmann, F.; Kuhn, D. Relative Binding Affinity Prediction of Farnesoid X Receptor in the D3R Grand Challenge 2 Using FEP+. J. Comput. Aided. Mol. Des. 2018, 32 (1), 265–272. https://doi.org/10.1007/s10822-017-0064-z.
- 肖高铿,李青松. 云计算教程 | 用FLARE FEP计算相对结合自由能. http://blog.molcalx.com.cn/2020/07/17/flare-fep.html
- Carvalho Martins, L.; Cino, E. A.; Ferreira, R. S. PyAutoFEP: An Automated Free Energy Perturbation Workflow for GROMACS Integrating Enhanced Sampling Methods. J. Chem. Theory Comput. 2021, acs.jctc.1c00194. https://doi.org/10.1021/acs.jctc.1c00194.
联系我们
我们不仅提供软件,还提供云计算资源与FEP计算服务。