摘要:本教程讲解了荧光发射光谱的形成过程、计算原理,并以荧光素为例,讲解了用Gaussian软件预测其发射荧光发射波长的流程,并将计算结果与实验观察到的发射波长进行比较以评估计算的精度。
作者:周经纬,肖高铿
一. 荧光计算的原理
荧光(fluorecence)属发射光谱,化合物吸收能量从基态(基态单重态、基态极小点构象)跃迁到激发态(激发态单重态、基态极小点构象),再以非辐射方式释放能量弛豫到激发态能量极小点(激发态单重态、激发态极小点构象),再以释放光子的方式(发射荧光)退激到基态(基态单重态,激发态极小点构象),如图1所示。
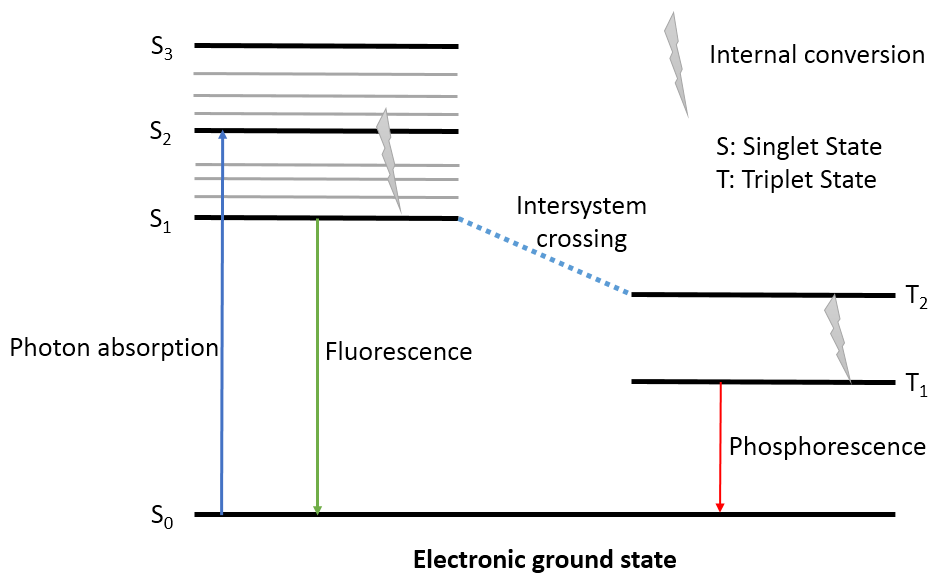
图1. 激发态与荧光、磷光
实际上,上述的过程可以用图2重新表述:
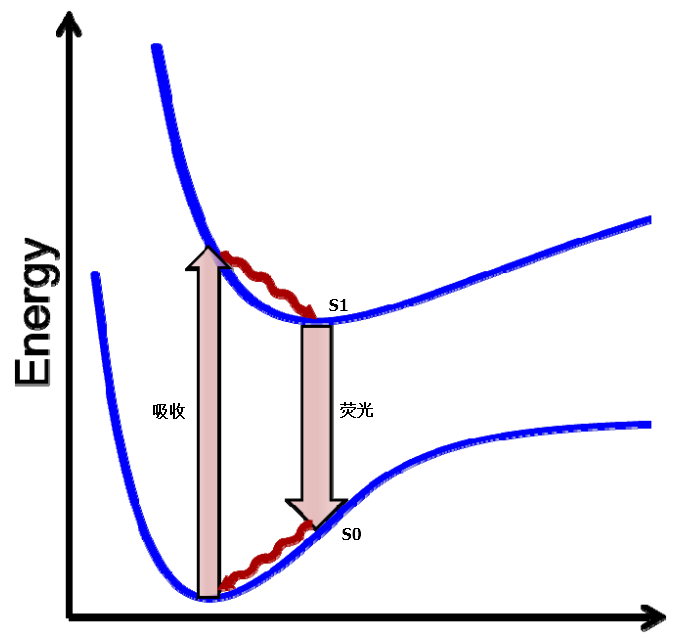
图2. 荧光是从激发态能量极小点退激到基态的过程,因此只要找到激发态能量极小点即可预测荧光波长
如图2所示,化合物从激发单重态S1退激为基态单重态S0时以光子的形式释放出能量,假定这份能量全部转化为光子,该光子的波长就对映着发射的荧光波长。在该过程中,S1与S0具有完全一样的构象,两者能量差值即是波长。
在Gaussian软件里,S1构象通过用TD-DFT对化合物单重态进行激发态优化获得。在TD计算时,Gaussian会以基态为参考,给出发射波长与能量,进行TD的Opt计算即可预测化合物的荧光波长。
从Gaussian 09 D.01或E.01的TD DFT计算结构很容易找到激发态,典型特征如下:
1 2 3 4 5 | Excited State 1: Singlet-A 2.4469 eV 506.71 nm f=1.0743 <S**2>=0.000 86 -> 87 0.70444 This state for optimization and/or second-order correction. Total Energy, E(TD-HF/TD-KS) = -1144.82946896 Copying the excited state density for this state as the 1-particle RhoCI density. |
This state for optimization and/or second-order correction是特征行,告诉我们需要找的地方在这里。其中第一行报告的2.4469 eV与506.71 nm即是发射光谱(荧光)的波长, 也等于激发态与基态能量差。
其中Total Energy即是激发态的能量,而基态能量可以从附近的SCF Done行找到或者从输出文件末尾“HF=”处找到:
1 2 | SCF Done: E(RB3LYP) = -1144.91938926 A.U. after 8 cycles NFock= 8 Conv=0.54D-08 -V/T= 2.0042 |
1 | .01\State=1-A\HF=-1144.9193893\RMSD=5.364e-09\RMSF=7.605e-06\Dipole=-0 |
表1. 激发态能量与基态能量
| 能量 | 单位 | |
| 激发态 | -1144.8294690 | Hartree |
| 基态 | -1144.9193893 | Hartree |
| ΔEnergy | 0.0899203 | Hartree |
| 2.4469 | eV |
激发态能量与基态能量差为2.4469eV,即为发射光谱(荧光)的波长506.71nm。
二. Gaussian计算的操作步骤
本计算以荧光素分子二钠盐为例说明荧光的计算过程,其2D结构如图3所示:
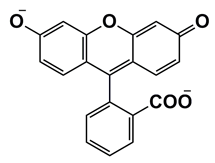
图3. 荧光素的结构
SMILES代码:[O-]C(=O)C1=CC=CC=C1C1=C2C=CC(=O)C=C2OC2=CC([O-])=CC=C12
水溶液荧光发射波长:512nm (臧运波等 2015)
水溶液荧光寿命:3.4ns
注:Chem3D、Markvin Sketch或Corina、OMEGA用户可以直接输入SMILES代码生成3D结构,推荐用CORINA或OMEGA生成3D结构MMFF94S力场优化后可以直接进行TD-DFT计算。
1. 3D结构的生成与优化
多种方式可以获得初始的3D结构进行计算:
- GaussView
- 用OMEGA等软件生成3D结构
- 用CONFLEX生成高质量的起始结构
可以用GaussView搭建3D结构,在基态下用小基组优化、再换成大的基组优化获得高质量初始结构进行TD-DFT计算。
用OMEGA等软件从1D的SMILES代码生成高质量的3D结构并进行构象搜索,取其全局极小点构象进行TD-DFT计算。OMEGA支持命令行,因此特别适合于在服务器上大规模化合物的计算。
CONFLEX可以穷尽的搜索化合物的构象,并计算构象分布,本文用CONFLEX对化合物在水溶液中进行构象搜索,取自由能最小的构象用于TD-DFT计算。
附CONFLEX–构象搜索教程:http://blog.molcalx.com.cn/2016/04/12/conflex-conformation-search.html
2. TD-DFT计算
获得初始构象后,采用TD-DFT进行结构优化计算, Route部分如下:
1 | # opt td=(nstates=5) apfd/6-311+g(2d,p) scrf=(solvent=water) |
为了快点看到计算结果,可以用更小的基组:
1 | # opt td=(nstates=5) B3LYP/6-31+G(d) scrf=(solvent=water) |
注意,电荷(Charge)与自旋多态性(spin multiplicity),本例中为分别为-2与1,更完整的输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | %nprocshared=32 %mem=64GB %chk=Fluorescein_S1_opt.chk # opt td=(nstates=5) b3lyp/6-31+g(d) scrf=(solvent=water) Structure: Fluorescein; OPT TD calculation at B3LYP/6-31+G(d) level -2 1 C -1.15448600 3.92565000 -0.43391700 C 0.20894200 3.50259100 -0.22848000 C 0.54581100 2.16421100 -0.18344700 ! 此处省略了很多molecule specification行 !空白行结束 |
3. 计算结果
我们可以找到最后一次出现的激发态计算的波长:
1 2 3 | Excited State 1: Singlet-A 2.4151 eV 513.36 nm f=1.0519 <S**2>=0.000 86 -> 87 -0.70463 This state for optimization and/or second-order correction. |
其中513.36nm即计算的发射波长(荧光),对应2.4151eV的能量, 与实验值512nm非常接近。
三. 相关教程
1. 磷光计算:http://blog.molcalx.com.cn/2016/05/22/oled-phosphorescence.html
2. 吸收光谱计算(UV,ECD):http://blog.molcalx.com.cn/2016/05/23/gaussian-ecd-tutorial.html
四. 文献
[1]臧运波,张爱梅. 荧光素钠-Mn~(2+)-H_2O_2体系荧光法测定常见水果的抗氧化活性[J]. 分析科学学报,2005,01:81-83.
[2]James B. Foresman and AEleen Frisch. Predicting Fluorescence: Optimizing Excited State Geometries. Exploring Chemistry with Electronic Structure Methods. Third Edition Page:347
五. 联系我们
电邮:info@molcalx.com
电话:020-38261356
单位:广州市墨灵格信息科技有限公司
网站:http://www.molcalx.com.cn/gaussian-09



