摘要:本教程介绍了范德华半径、范德华表面、分子体积、溶剂半径和蒙特卡罗方法等相关概念。并以甲烷分子为例,详细介绍了如何利用Gaussian程序计算分子的范德华体积,以及自定义溶剂模型时使用的溶剂半径。
作者:陈宇
时间:2020年1月1日
基本概念
范德华半径(van der Waals radius)
在理想状态下,当两个以范德华力结合在一起的相同原子处于平衡状态时,那么这两个原子之间距离的一半就定义为范德华半径。
范德华表面(van der Waals surface)
对于一个分子,其中的原子可以看成以范德华半径为半径的小球,这些小球堆积在一起,会使不同球的表面互相连接成一个连续的表面,这个表面就称为范德华表面,它是一个闭合的曲面,包裹了整个分子。然而在分子中,由于电荷会发生转移,这种方法定义的范德华表面会有不合理之处,现在常用的范德华表面是由Bader提出的由0.001 electrons/Bohr3电子密度构成的等值面(一般在气相中,使用0.001 electrons/Bohr3,而在凝聚相中使用0.002 electrons/Bohr3)。
分子体积(Molecular Volume)
分子体积的定义依赖于我们如何定义分子的范围,通常我们把分子范德华表面围成的体积定义为分子体积,也称为分子的范德华体积,而其中最常用的范德华表面就是Bader提出的0.001 electrons/Bohr3电子密度构成的等值面(气相状态下)。
蒙特卡罗方法(Monte Carlo method)
Gaussian使用蒙特卡罗方法计算分子的体积,因此我们在此简要介绍蒙特卡罗方法的核心思想,体验一下简单思想带来的巨大力量。下面图1a是一张中国地图,请问如何计算其面积?由于边境线的不规则,常规的计算公式很难发挥作用。蒙特卡洛方法的核心思想在于通过大量的随机采样来逼近研究对象的真实轮廓,我们可以先用一个矩形将地图完全围住(如图1b),然后随机的在上面撒上一把砂粒(也可以每次只抛一粒,重复多次),接下来我们需要记录停在地图轮廓内部的沙粒数目n,以及整个矩形内部所有的沙粒数m,然后计算出矩形的面积V,则地图的面积可以近似为n/m*V,当沙粒越密集时,得到的计算值就越接近于真实结果。而对于计算体积,只是相当于从二维空间扩展到了三维空间。
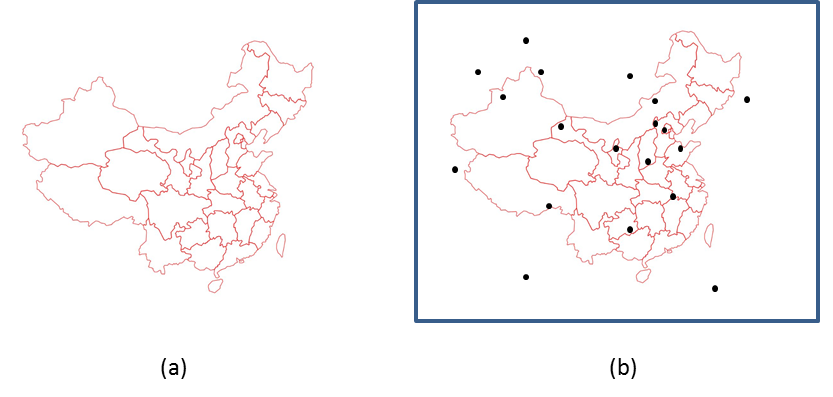
图1 蒙特卡罗方法示意图
利用Gaussian程序计算分子体积的流程
Gaussian程序提供了Volume关键字来进行分子体积的计算,在这个教程中我们将以甲烷(CH4)分子为例,演示如何计算气相条件下分子的体积,以及其中要注意的一些事项。
计算分子体积的基本流程:
- 优化分子结构
- 体积计算
- 读取结果
使用优化好的分子作为初始结构,用更大的方法基组计算分子体积。
体积计算的具体操作步骤
第一步:优化CH4分子的结构
CH4分子结构的输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | %mem=1GB %nproc=8 # M06/6-31G(d) opt freq CH4 0 1 C 1.84838172 -0.97955706 0.00000000 H 2.20503615 -1.98836706 0.00000000 H 2.20505456 -0.47515887 0.87365150 H 2.20505456 -0.47515887 -0.87365150 H 0.77838172 -0.97954387 0.00000000 !空白行不可忽略 |
第二步:CH4分子体积的计算
使用第一步优化得到的结构作为初始结构,用M06/6-311++G(d,p)方法基组计算CH4分子的体积。输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | %mem=1GB %nprocshared=8 # m06/6-311++G(d,p) volume iop(6/45=20) CH4 0 1 C 0.00000000 0.00000000 0.00000000 H 0.63141200 0.63141200 0.63141200 H -0.63141200 -0.63141200 0.63141200 H -0.63141200 0.63141200 -0.63141200 H 0.63141200 -0.63141200 -0.63141200 !空白行不可忽略 |
第3行为Route行,关键字Volume指示Gaussian进行体积计算;用IOP设置随机撒点的密度,这里设置为20,相当于每立方波尔平均有20个随机点,这也是默认的选项。
第三步:读取计算结果
可以用文本编辑器打开输出文件,在其中找到下述几行:
1 2 3 4 5 6 7 8 9 10 | Monte-Carlo method of calculating molar volume: based on 0.001 e/bohr**3 density envelope. Number of points per bohr**3 = 20 CutOff= 1.00D-04 Using the SCF density. There are 260 points. Will hold 260 in memory. LenV= 1342160379 MDV= 1342177280. Box volume = 2209.956 fraction occupied=0.158 Integrated density= 9.5164379903287593D+00 error=-4.8356200967124074D-01 Molar volume = 348.493 bohr**3/mol ( 31.099 cm**3/mol) Recommended a0 for SCRF calculation = 3.04 angstrom ( 5.75 bohr) |
其中第9行Molar volume = 348.493 bohr**3/mol给出最终计算的分子体积为:348.493 Bohr3。
其中第10行 SCRF calculation = 3.04 angstrom给出了Onsager溶剂反应场模型的溶剂半径,也就是在溶剂化计算中,如果需要自定义溶剂,那么溶剂半径可以使用这个值。
随机撒点数与范德华表面定义对体积计算的影响
在上面地图面积计算的例子中,我们提到影响计算结果的因素是沙粒的密集程度。同样,在我们计算分子体积时,这也是一个关键因素。此外,我们还提到,范德华表面定义的不同也会影响计算出的分子体积。因此,下面我们将调整这两个参数,以便观察它们对计算结果的影响。
1. 调整随机撒点的数量计算分子体积
首先,我们将随机撒点的数量调整到平均2000每立方波尔,输入文件如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | %mem=1GB %nprocshared=8 # m06/6-311++G(d,p) volume iop(6/45=2000) CH4 0 1 C 0.00000000 0.00000000 0.00000000 H 0.63141200 0.63141200 0.63141200 H -0.63141200 -0.63141200 0.63141200 H -0.63141200 0.63141200 -0.63141200 H 0.63141200 -0.63141200 -0.63141200 !空白行不可忽略 |
第3行为Route行,关键字Volume指示Gaussian进行体积计算;用IOP设置随机撒点的密度,这里设置为2000,相当于每立方波尔平均有2000个随机点。
2.改变范德华表面的定义
接下来,我们将范德华表面的电子密度设置为0.002(默认为0.001),再计算分子体积,输入文件分别如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | %mem=1GB %nprocshared=8 # m06/6-311++G(d,p) volume iop(6/45=2000,6/46=20) CH4 0 1 C 0.00000000 0.00000000 0.00000000 H 0.63141200 0.63141200 0.63141200 H -0.63141200 -0.63141200 0.63141200 H -0.63141200 0.63141200 -0.63141200 H 0.63141200 -0.63141200 -0.63141200 !空白行不可忽略 |
第3行为Route行,关键字Volume指示Gaussian进行体积计算;范德华表面由Bader提出的由0.001 electrons/Bohr3电子密度构成的等值面来定义,IOP 6/46=20将电子密度等值面设置为0.002。
3. 结果分析
在表1中,我们列出了不同参数下得到的分子体积。
表1. 不同参数下分子体积的计算结果
| 参数 | 电子密度:0.001 随机点数:20 | 电子密度:0.001 随机点数:2000 | 电子密度:0.002 随机点数:2000 |
|---|---|---|---|
| 体积(bohr3) | 348.493 | 288.513 | 216.491 |
从上面的结果可以看出,当随机点设置为默认的20时,与设置为2000时有很大的差距,这也意味着在实际的研究中,如果使用默认设置,很可能导致较大误差,在计算资源允许的情况下应该确保较大的随机点数。在这里也不推荐设置较小的随机点数,然后多次计算取平均值的做法。
可以看到,当电子密度设置为0.002时,在同样的随机点数下,分子体积也变小,这是因为范德华表面更贴近原子核,使得包围的空间变小的缘故。
参考资料
- http://gaussian.com/volume



