摘要：电子密度差图常用于激发态跃迁的结果分析, 然而有时电子密度差图并不能清楚、确切给出结果，此时，自然跃迁轨道(Natural transition orbitals, NTOs)可能就能帮上忙。本教程演示了如何进行NTOs计算：激发态计算，确定NTO分析的激发态，NTOs计算。

原文：http://www.gaussian.com/g_blog/faq4.htm
改编：肖高铿

一. 自然跃迁轨道简介

Gaussian的TD-DFT方法为激发态的研究提供了非常实用的方法，因为它的结果与DFT计算研究基态一样精确。电子密度差图常用于激发态跃迁的结果分析(见教程：Gaussian教程–GaussView绘制电子密度差图)。然而有时电子密度差图并不能清楚、确切给出结果，此时，另一种技术–自然跃迁轨道(Natural transition orbitals, NTOs)可能就能帮上忙。

NTOs是一种定性描述电子激发便利的方法，从TD能量计算的跃迁密度开始可以非常快速地计算获得NTOs。NTOs将经典的轨道转化为紧凑的形式，将每个激发态跃迁用一对或两对的轨道表示：NTOs跃迁从激发的占据轨道（occupied transtion orbitals,也称为hole）跃迁到非占据跃迁轨道(unoccupied transtion orbitals,也称为particle或electron)。当一个激发态不存在单个优势轨道跃迁，需要用很多轨道系数相近的经典轨道跃迁来描述的时候，此时若电子密度差不能清楚归属跃迁性质，NTOs经常可以帮上大忙。更详细的NTOs介绍，参见文献[Martin03]。

二. 如何计算NTOs

三步完成NTOs计算:

  1. TD-DFT计算激发态，保存checkpoint文件
  2. 检查计算结果，确认需要分析的激发态
  3. 单点计算生成感兴趣激发态的NTOs

对于不同激发态的NTOs：重复计算第三步。

三. 操作步骤

1.激发态计算

第一步激发态计算例子如下。这是一个TD-DFT计算，在这之前已经被优化并确认是一个极小点结构。

1
2
3
4
5
6

%Chk=tddft
# B3LYP/6-311+G(d,p) TD(NStates=40) 
 
TD-DFT excited state calculation: B3LYP/6-311+G(2d,p)
 
!此处省略了molecule specification部分

2. 确认需要分析的激发态

假设，我们对第3激发态感兴趣，并对该激发态进行NTOs分析。

3. NTOs生成与可视化分析

现在，我们需要进行计算以生成NTOs并提供给GaussView进行可视化分析。
在本例中，我们需要计算第三激发态的NTOs：

1
2
3

%OldChk=tddft
%Chk=state3
# B3LYP/6-311+G(2d,p) Geom=AllCheck Guess=(Read,Only) Density=(Check,Transition=3) Pop=(Minimal,NTO,SaveNTO)

Pop=NTO选项告诉Gaussian进行NTO计算，Pop=SaveNTO选项告诉Gaussian将Checkpoint文件中基态的轨道替换为计算获得的NTOs。GaussView可以用于展示checkpoint文件中的任意轨道，包括NTOs，所以使用GaussView的时候无需做任何特殊修改或设置。

如果想生成第6激发态的NTOs，可以在上面的输入文件里通过Link1加入该作业：

1
2
3
4

--Link1--
%OldChk=tddft
%Chk=state6
# B3LYP/6-311+G(2d,p) Geom=AllCheck Guess=(Read,Only) Density=(Check,Transition=6) Pop=(Minimal,NTO,SaveNTO)

四. 举例

1. Pt(dcbpy)Cl2的激发态计算

Pt(dcbpy)Cl2结构如图1所示：
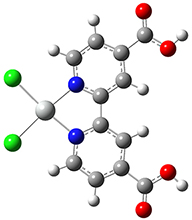
如何产生自然跃迁轨道：Pt(dcbpy)Cl2

图1.Pt(dcbpy)Cl2的结构

计算细节（见Roy09）：
route部分：TD(NStates=40) CAM-B3LYP/Gen Pseudo=Read
基组(ECPs): Pt用LANL08，其它原子用6-311G(d)

TD-DFT计算获得第19激发态结果如下:

1
2
3
4
5
6
7
8
9

 Excited State 19: Singlet-A  4.7936 eV  258.64 nm  f=0.0002 …
      78 -> 90         0.41835
      78 -> 92        -0.18686
      78 -> 95         0.17948
      79 -> 91         0.42043
      79 -> 94        -0.10009
      79 -> 99         0.12527
      80 -> 90         0.15807
      87 -> 92         0.11388

根据该激发态跃迁的各个轨道系数, 没有一个跃迁占绝对优势。下图2展示了分子轨道及其跃迁，并标注上了对应的系数：
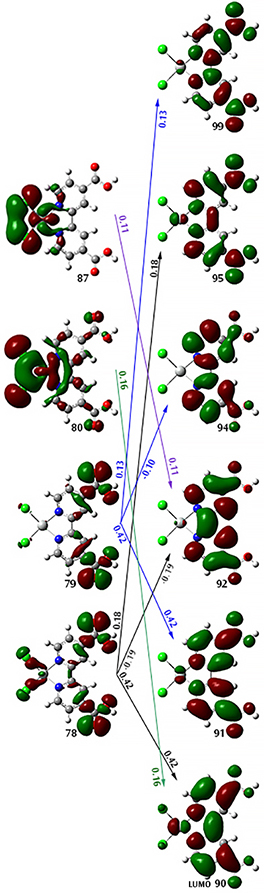
如何生成NTO：分子轨道与跃迁

图2.Pt(dcbpy)Cl2的分子轨道与跃迁

但是对该激发态进行NTOs计算，获得两对NTOs（如图3、4所示），可以极大地简化了跃迁过程的表征：
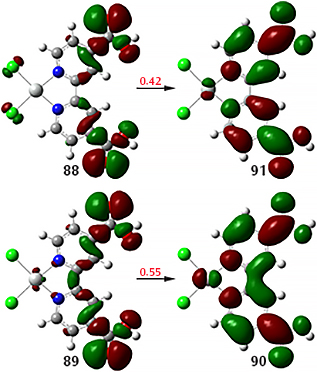
如何生成NTOs：两对NTOs

图3.Pt(dcbpy)Cl2的两对NTOs

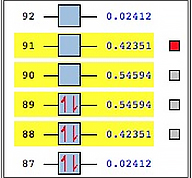
如何产生自然跃迁轨道：两对NTOs

图4. Pt(dcbpy)Cl2的两对NTOs

五. 文献

[Martin03] Martin, R. L. “Natural transition orbitals.” JCP 2003, 118, 4775-4777. doi:10.1063/1.1558471

[Roy09] Roy, L. E.; Scalmani, G.; Kobayashi, R.; Batista, E. R.“Theoretical studies on the stability of molecular platinum catalysts for hydrogen production.” Dalton Trans. 2009, 6719–6721. doi:10.1039/b911019b