摘要:本文研究了局部反应性描述符在理解药物代谢方面的实用性。计算了18种药物和11种农用化学品的亲电型福井函数,并讨论了其与实验观测到的代谢产物之间的关系。在许多实例中,福井函数的极大值对应于代谢攻击的主要位点,有助于对实验结果进行事后解释。在论文的第二部分,作者在福井函数框架下探讨了细胞色素中亲电氧化物种"复合物I"(Compound I, Cpd I)的本质。通过计算涉及Cpd I相关自旋态的亲核型福井函数,实现了对其反应性的更定性、更直观的理解。
原文:Beck ME. Do Fukui function maxima relate to sites of metabolism? A critical case study. J Chem Inf Model. 2005 Mar-Apr;45(2):273-82. doi: 10.1021/ci049687n. PMID: 15807488.
编译:肖高铿
前言
理解一种药物或农用化学品的代谢命运及其行为,对于此类化学物质的开发至关重要,因为代谢、吸收、分布及排泄共同决定了其生物利用度、药效、不良反应以及毒理学特性。
目前存在多种计算方法,可用于事后或前瞻性地理解代谢和/或毒性。这些方法通常基于分子描述符(通常是拓扑描述符)进行统计建模[1-3]。细胞色素在代谢过程中扮演着重要角色,因为大多数氧化性代谢反应均由这类酶催化(参见参考文献4和5中关于实验与理论研究的综述)。随着细胞色素X-衍射晶体结构的获得,已发展出三维定量构效关系(3D-QSAR)模型(例如参见参考文献6-9)。另一种方法是基于配体的,通过量子化学计算预测优先的拔氢位点(例如参见参考文献10和11)。
最直接但也是最具挑战性的方法,无疑是采用量子化学手段对细胞色素介导的羟基化全过程进行建模[5,12,13]。在最近的一项此类计算中(本研究全文以此为参照),羟基化过程通过量子力学/分子力学(QM/MM)耦合方法进行了模拟。这些计算有力支持了“双态反应性”模型(two-state reactivity,TSR),该模型认为细胞色素活性位点中的潜在氧化物种——“复合物I”(Compound I,Cpd I)——是一种具有双重态(doublet)或四重态(quartet)自旋耦合的自由基物种。该反应以两步“反弹机制”(rebound mechanism)进行:第一步是底物中氢原子的拔出,其在双重态下的活化能垒略低于四重态;第二步是羟基加成到底物上,在双重态下几乎无能垒,而在四重态下则需要一定的活化能。
据作者所知,首次且唯一将DFT衍生的反应性描述符应用于生物体系的研究是文献15,该研究将硬软酸碱(HSAB)原理[16]应用于砷酸还原酶和低分子量磷酸酶的无机模型体系。
在本研究中,对若干已知代谢产物的药物和农用化学品计算了福井函数[17]。旨在探讨福井函数的最大值在多大程度上可与实际观测到的代谢位点相关联,目标是建立定性而非定量的关系。论文的第二部分则针对Cpd I的模型体系计算了福井函数,其目的在于获得对该难以捉摸物种性质的定性、化学直觉上的深入理解。
理论
一些来自概念性密度泛函理论(Conceptual DFT)的结果[17-21]
众多关于一般化学反应性的概念已广为人知,例如软硬酸碱理论[16,22] 、电负性[23-25]、以及前线轨道理论[26-28]。这些概念在密度泛函理论(DFT)中获得了坚实的理论基础,尤其是通过Yang和Parr的工作得以确立[18,17]。
除了其形式上的优美之外,该理论还具有另一个优点:相关计算相对容易实现。在DFT框架下,化学势 μ 和硬度 η 可表示为系统能量 E 对外势场 V(r)(即原子核构型)以及电子数 N 的泛函偏导数:
$$
\mu = \left( \frac{\partial E}{\partial N} \right)_{V(\mathbf{r})} \qquad(1)
$$
$$
\eta = \left( \frac{\partial^{2} E}{\partial N^{2}} \right)_{V(\mathbf{r})} \qquad(2)
$$
电子密度 ρ(r),定义为在粒子数 N不变的条件下,体系能量 E对外部势场 V(r)的泛函导数:
$$
\rho(\mathbf{r}) = \left( \frac{\delta E}{\delta V(\mathbf{r})} \right)_{N} \qquad(3)
$$
可以证明,当电子密度 ρ(r) 在给定外势场 V(r) 下使系统能量 E 达到最小值时,硬度 η 取得最大值。硬度是一个与化学反应性相关的全局参数。
在有限差分方法中,硬度可近似表示为:
$$
\eta\approx\frac{\mathrm{IP}-\mathrm{EA}}{2}\qquad(4)
$$
其中:
$$
\mathrm{IP}=E[N-1,V(\mathbf{r})]-E[N,V(\mathbf{r})]\approx\mu^{-}\qquad(5)
$$
$$
\mathrm{EA}=E[N,V(\mathbf{r})]-E[N+1,V(\mathbf{r})]\approx\mu^{+}\qquad(6)
$$
分别是垂直电离能(vertical ionization potential)和垂直电子亲和能(vertical electron affinity)。
闵克尔(Mulliken)的电负性为:
$$
\chi=\frac{\mathrm{IP}+\mathrm{EA}}{2}\approx-\mu^{0}\qquad(7)
$$
如公式5-7所示,电离能(IP)、电子亲和能(EA)以及电负性(χ)可被视为化学势 \(μ = (∂E/∂N)_{V(r)}\) 的左导数、右导数和平均导数的有限差分近似。
反应性的局域参数——福井函数(Fukui function),则是通过能量对电子数 N 和外势场 V(r) 的混合偏导数得到的:
$$
\begin{align*}
f^{\pm}(\mathbf{r})&=\left(\frac{\delta^{2}E}{\partial N\delta V(\mathbf{r})}\right)^{\pm}\\
&=\left(\frac{\partial\rho(\mathbf{r})}{\partial N}\right)^{\pm}_{V(\mathbf{r})}
\end{align*}\qquad(8)
$$
同样,如正负号(±)所示,右导数与左导数是不同的。
在实际计算中,福井函数通过有限差分法求得:
$$
\begin{aligned}
f^{+}(\mathbf{r}) &\approx \rho(N+1,\mathbf{r})-\rho(N,\mathbf{r}) \\
f^{-}(\mathbf{r}) &\approx \rho(N,\mathbf{r})-\rho(N-1,\mathbf{r})
\end{aligned} \qquad(9)
$$
其中所有电子密度均在固定外势场 \( V(\mathbf{r}) \) 下计算。
\( f^{+} \) 的极大值指示分子中易受亲核试剂进攻的区域,而 \( f^{-} \) 的极大值则出现在易受亲电试剂进攻的位置。换言之,\( f^{+} \) 表明电子密度增加在能量上更有利的区域,而 \( f^{-} \) 在电子密度减少更被偏好之处达到最大。
有助于理解全局反应性与局域反应性之间相互作用的一个方程是:
$$
d\mu=2\eta\mathrm{d}N+\int d\mathbf{r}\,f(\mathbf{r})\mathrm{d}V(N,\mathbf{r}) \qquad(10)
$$
该式将一个基态向另一个基态转变时化学势的变化,分别通过硬度(hardness)和福井函数与电子数的变化以及外势场的变化联系起来。
应当注意,此处所采用定义中的福井函数仅将反应性的描述局限于电子方面。若考虑原子核的位移(参见参考文献29和30及其引用的文献),则可获得更完整的反应性图像。
福井函数与代谢位点可能相关的理由
如前言中粗略所述,细胞色素介导的代谢性羟基化作用归因于一个铁氧代物种复合物I(Cpd I)。根据现有知识,Cpd I 可被视为一种“亲电性氧化剂”。因此,对底物计算得到的 \( f^{-} \) 函数应有助于识别分子中易被 Cpd I 攻击的位置;反之,对 Cpd I 计算得到的 \( f^{+} \) 函数则应显示 Cpd I 易被底物进攻的部位。已有研究成功地将农用化学品的半经验计算所得原子HOMO系数与氧化性代谢路径相关联[31,32]。该方法本质上等价于在冻结轨道近似下计算 \( f^{-} \) 函数,此时 \( f^{-} \) 简化为HOMO电子密度。
此类方法最明显的缺陷显而易见:福井函数描述的是对一个各向同性、抽象的“反应性环境”的反应性。如果药物在细胞色素活性位点中处于特定取向,其氧化反应将不会发生在与各向同性条件(例如,在溶液中,或与体积小、空间位阻较小的反应物作用时)相同的分子位置上。这是所有“基于配体”方法普遍存在的缺陷。
方法
本研究中对所有药物均采用以下流程:首先生成一个“合理”的初始几何构型,随后使用Sybyl软件35中实现的MMFF94s力场33,34对其进行优化。通过一种自研方法对扭转构象空间进行探索,该方法结合了蒙特卡罗步骤与模拟退火技术36。从MMFF94能量最优的构象中,人工选择一个作为代表。对于部分化合物,研究了两个至四个不同的几何构型。福井函数在不同构象间变化不大(即极大值位置在各构象中均位于相同的官能团上)。因此,后续仅报告一个构象的结果。
所选构象在RI-DFT理论水平下进行全几何优化37-39 。采用Becke与Perdew的泛函组合40,41。所有原子均分配Ahlrichs的TZVP基组42 。溶剂效应通过COSMO模型43 估算。采用80.2(水)和4.0(酶内部)的介电常数,以模拟水溶液与蛋白质环境之间的差异。全局反应性指标对介电常数的依赖性在小介电常数\(ε < 4.0\)时最为显著44。凝聚态福井函数表现出明显但不剧烈的介电效应45,46。在本研究计算中,福井函数对介电常数的选择并不敏感;因此,此处仅报告ε = 4.0的结果。所有上述及后续的DFT计算均使用Turbomole程序包47完成。
在已获得的几何结构基础上,采用与前述相同的泛函和基组进行单点非限制RI-DFT计算:分别对中性物种(N个电子)、自由基阳离子(N−1个电子)和阴离子(N+1个电子)各执行一次计算。通过自旋期望值估算自旋污染程度,结果表明在所有研究体系中自旋污染均处于合理水平(见表1)。
| object | M (anion) | M (neutral) | M (cation) | IP (kcal) | EA (kcal) | \(-\mu^{0}=\chi\) (kcal) | η (kcal) |
|---|---|---|---|---|---|---|---|
| adinazolam | 2.0028 | 1.0000 | 2.0023 | 152.0 | 46.3 | 99.1 | 52.9 |
| azelastine | 2.0038 | 1.0000 | 2.0022 | 144.5 | 37.5 | 91.0 | 53.5 |
| celecoxib | 2.0021 | 1.0000 | 2.0064 | 161.6 | 43.8 | 102.7 | 58.9 |
| Δ8-tetrahydrocannabinol | 2.0025 | 1.0000 | 2.0063 | 143.1 | 5.3 | 72.4 | 68.9 |
| dexamethasone | 2.0060 | 1.0000 | 2.0023 | 153.9 | 37.1 | 95.5 | 58.4 |
| diclofenac | 2.0037 | 1.0000 | 2.0053 | 142.9 | 21.8 | 82.4 | 60.6 |
| estradiol-3-methyl ether | 2.0027 | 1.0000 | 2.0037 | 146.2 | 4.9 | 75.6 | 70.7 |
| etoposide-3-methyl ether | 2.0024 | 1.0000 | 2.0023 | 135.3 | 16.0 | 75.7 | 59.6 |
| felodipine | 2.0023 | 1.0000 | 2.0100 | 146.2 | 38.0 | 92.1 | 54.1 |
| flurbiprofen | 2.0025 | 1.0000 | 2.0032 | 157.2 | 29.8 | 93.5 | 63.7 |
| lorsatan | 2.0026 | 1.0000 | 2.0034 | 152.8 | 28.8 | 90.8 | 62.0 |
| MN-1695 | 2.0037 | 1.0000 | 2.0039 | 161.1 | 36.2 | 98.7 | 62.4 |
| phenprocoumon | 2.0030 | 1.0000 | 2.0033 | 154.5 | 39.4 | 96.9 | 57.6 |
| phenytoin | 2.0026 | 1.0000 | 2.0027 | 154.5 | 36.4 | 95.5 | 59.0 |
| pranidipine | 2.0032 | 1.0000 | 2.0068 | 165.5 | 30.5 | 98.0 | 67.5 |
| S-MTTPPA | 2.0026 | 1.0000 | 2.0047 | 157.6 | 36.7 | 101.3 | 64.6 |
| taxol | 2.0038 | 1.0000 | 2.0010 | 153.8 | 37.4 | 95.6 | 58.2 |
| warfarin | 2.0031 | 1.0000 | 2.0036 | 165.7 | 20.7 | 93.2 | 72.5 |
| carbopropamid | 2.0041 | 1.0000 | 2.0019 | 163.1 | 15.4 | 89.2 | 73.9 |
| chlorpropifos | 2.0037 | 1.0000 | 2.0024 | 189.5 | 7.0 | 98.2 | 91.3 |
| fentrazamide | 2.0030 | 1.0000 | 2.0022 | 165.5 | 30.5 | 98.0 | 67.5 |
| imidacloprid | 2.0030 | 1.0000 | 2.0033 | 165.9 | 36.7 | 101.3 | 64.6 |
| parathion | 2.0028 | 1.0000 | 2.0034 | 198.6 | 20.5 | 109.6 | 89.0 |
| propazine | 2.0032 | 1.0000 | 2.0018 | 166.1 | 28.7 | 97.4 | 68.7 |
| spiroxamine | 2.0009 | 1.0000 | 2.0020 | 139.2 | 15.2 | 62.0 | 77.2 |
| thiacloprid | 2.0039 | 1.0000 | 2.0050 | 147.9 | 33.8 | 92.0 | 58.0 |
| thiabendazole | 2.0039 | 1.0000 | 2.0093 | 167.9 | 32.8 | 99.9 | 67.1 |
a. 表格右半部分报告了根据公式4至7定义的所有非限制性DFT计算所得的全局反应性参数和多重度。
在0.5 Å分辨率的矩形网格上,对N和N−1电子物种的电子密度进行了数值计算。通过有限差分法(见公式9),从这些网格数据中计算出f⁻ 福井函数,并使用Molcad软件48进行可视化分析(见图2)。
表1还总结了所评估药物的硬度(η)、电负性(χ)、电离势(IP)以及电子亲和能(EA)等数值。此处列出这些值仅出于完整性考虑;由于本研究并不旨在对代谢速率等进行定量预测,因此不再进一步讨论这些数值。
在对Cpd I进行福井函数计算时,该方法进行了相应调整。在药物的计算中,N电子物种为单重态,因此N±1电子物种必然是双重态。然而根据TSR模型,Cpd I的相关自旋态应为双重态(²A)和四重态(⁴A)。当N电子物种的多重度\(M > 1\)时,增加一个电子可能产生M+1或M−1的多重度,移除一个电子亦然。因此,在缺乏证据排除M+1或M−1的情况下,对于给定的多重度\(M > 1\),需考虑两种f⁻和两种f⁺ 福井函数,也就是:
$$
\begin{aligned}
f_{M}^{+ \uparrow}(\mathbf{r}) &\approx \rho^{M+1}(N+1,\mathbf{r})-\rho^{M}(N,\mathbf{r}) \\
f_{M}^{+ \downarrow}(\mathbf{r}) &\approx \rho^{M-1}(N+1,\mathbf{r})-\rho^{M}(N,\mathbf{r}) \\
f_{M}^{- \uparrow}(\mathbf{r}) &\approx \rho^{M}(N,\mathbf{r})-\rho^{M+1}(N-1,\mathbf{r}) \\
f_{M}^{- \downarrow}(\mathbf{r}) &\approx \rho^{M}(N,\mathbf{r})-\rho^{M-1}(N-1,\mathbf{r})
\end{aligned}
\tag{11}
$$
其中箭头 \(\uparrow\) 和 \(\downarrow\) 分别表示多重度增加和减少一个单位。Cpd I 的 \(^{2}A\) 和 \(^{4}A\) 态对应 M=2 和 M=4。乍一看,这种程序可能让部分读者联想到参考文献 50 和 51。这些作者发展了一套在 \(\{N, N_{S}, V(\mathbf{r})\}\) 空间中的反应性理论,其中 \(N_{S} = N_{\alpha} – N_{\beta}\)。由此得到的福井函数 \(f_{NN} = (\partial\rho/\partial N)_{N_{S},V}\) 和 \(f_{NS} = (\partial\rho/\partial N_{S})_{N,V}\) 不应与式 (11) 混淆,后者仍处于 \(\{N, V(\mathbf{r})\}\) 的图像框架中。
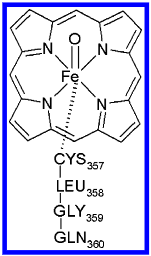
图1. Cpd I的模型体系
为了获得 Cpd I 模型体系的亲核性福井函数 \(f_{2}^{+ \uparrow}\) 和 \(f_{4}^{+ \uparrow}\),通过单点非限制性 RI-DFT/BP86 计算获得了电子密度 \(\rho^{1}(N+1,\mathbf{r})\)、\(\rho^{2}(N,\mathbf{r})\)、\(\rho^{3}(N+1,\mathbf{r})\)、\(\rho^{4}(N,\mathbf{r})\) 和 \(\rho^{5}(N+1,\mathbf{r})\)。该模型体系构建自 Schöneboom 等人12通过 QM/MM 优化得到的 Cpd I 蛋白复合物几何结构,他们慷慨提供了坐标文件。该计算始于实验测定的 CYP P450cam 的 X 射线结构52。在此几何中,除血红素部分(包括 Fe=O 基团)以及距离硫桥最近的四个蛋白残基(CYS357、LEU358、GLY359 和 GLN360)外,其余所有原子均被移除(见图 1)。开放价键由氢原子饱和。采用 COSMO 模拟介电常数为 \(\epsilon=4.0\) 的环境。对于氨基酸残基使用 SVP 基组;四吡咯体系的原子用 TZVP 基组;\(\mathrm{S-Fe}=\mathrm{O}\) 片段用 TZVPP 基组42。为处理铁原子的内层电子,使用有效核心势方法(ECP)53(ECP 基组 (8S7P6D)/[6S5P3D]54)。
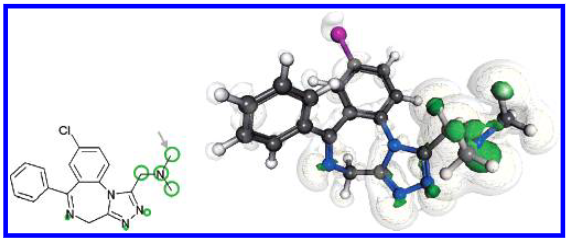
图2. 阿地那唑仑(adinazolam)的亲电型福井函数 \(f^{-}\) 。等值线图:等值线水平为 0.005(绿色,不透明)、0.001(黄色,网状)、0.0005(白色,透明)。在本图及后续各图中,灰色箭头表示代谢羟基化的位点;对于非羟基化反应,这些位点或明确标出,或以灰色圆圈表示。灰色“闪电”符号代表键的断裂。绿色圆圈为 \(f^{-}\) 函数极大值的示意图。详见正文。
| electrons | target multiplicity | actual multiplicity |
|---|---|---|
| N | quartet | 4.0123 |
| N | doublet | 2.8317 |
| N | doublet* | 2.0001 |
| N | triplet | 3.0157 |
| N + 1 | singlet | 1.0001 |
| N + 1 | triplet | 3.0157 |
| N + 1 | quintet | 5.0243 |
a. 注意:非限制性计算在双线态上的自旋污染程度极大。星号表示该计算采用了自旋湮灭技术,详见正文。
遗憾的是,对双重态进行的非限制性计算所得电子密度受到高多重度态的强烈污染。根据 \(\langle\hat{S}^{2}\rangle\) 期望值推导出的多重度在上述理论水平下为 2.83。由于此类污染可能破坏由此类密度导出的福井函数,因此对双重态的非限制性计算应用了自旋湮灭技术55,56。表 3 总结了所得自旋性质。
| participating Model states | singlet N + 1 | triplet N + 1 | quintet N + 1 |
|---|---|---|---|
| doublet* (N) | 86.5 | 114.0 | quintet N + 1 |
| quartet (N) | 86.5 | 103.4 | 83.5 |
a. 与表2采用相同的命名规范。仅考虑了自旋投影计算所得的能量。对于中性双线态,计算采用了自旋湮灭技术,详见正文。
已知12,13,四重态与双重态的几何结构非常相似。此外,卟啉的丙酸侧链并不携带显著的自旋密度。基于这些结果(在本文所报告计算完成后才发表),对模型体系的选择提供了合理依据。事实上,该模型体系避免了其他(尤其是气相模型体系)计算中的缺陷——在那些体系中,自旋密度在硫原子、四吡咯体系与 Fe=O 基团之间的分布与蛋白复合物中的实际情况定性不同12,57。
福井函数的可视化方式如前所述。此外,还计算了双重态和四重态的自旋差分密度:
$$
\Delta \rho ^{M}(N, \mathbf{r})=\rho ^{M}(N_{\alpha }, \mathbf{r})-\rho ^{M}(N_{\beta }, \mathbf{r}) \qquad (12)
$$
其中\(N=N_{\alpha}+N_{\beta}\),并假设 \(N_{\alpha}\geq N_{\beta}\)。
结果与讨论
药物
图3展示了阿地那唑仑(Adinazolam)的亲电福井函数 \(f^-\)。对于另外17种药物,仅提供了亲电福井函数的示意图(见图3)。所有福井函数的可视化结果可作为支持信息获取。示意图的排列顺序与文中讨论相应药物的顺序一致。
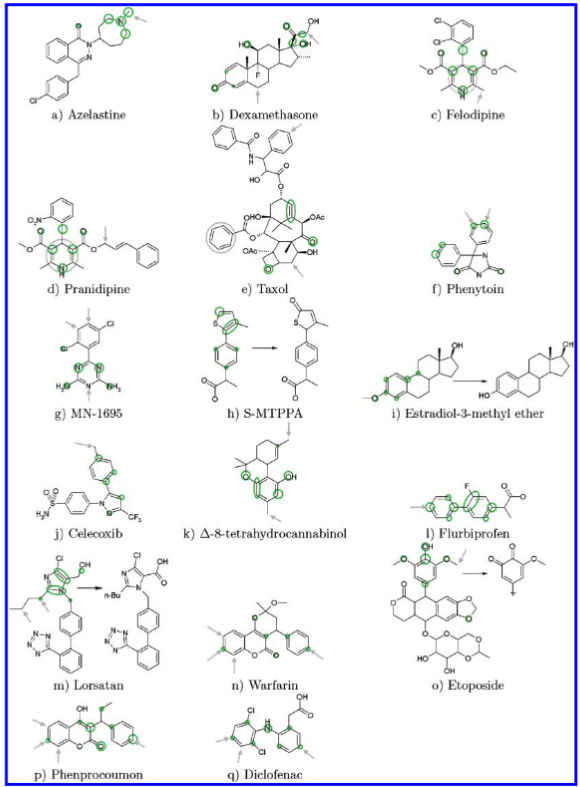
图3. 17个药物的亲电型福井函数 \( f^{-} \) 示意图。灰色箭头表示代谢羟基化的位点;对于非羟基化反应,这些位点或明确标出,或以灰色圆圈表示。灰色“闪电”符号代表键的断裂。绿色圆圈表示 \( f^{-} \) 函数的极大值位置。详见正文。
第一个药物实例——阿地那唑仑至紫杉醇(图2和图3a-e)——数据来源于 Singh 等人11。对于这些化合物,通过半经验方法估算的拔氢能与羟基化位点之间已得到相当成功的相关性11。其余化合物(图3f-q)则已由 Zamora 等人9利用三维定量构效关系(3D-QSAR)模型进行过研究。
已知阿地那唑仑存在多种代谢产物58,它们均源于对叔胺基团的进攻,这与 \(f^-\) 的预测结果一致(见图2)。对于阿泽拉司汀(azelastine,图3)的计算也正确提示了类似的反应路径,但忽略了6位上的羟基化反应59,60。
在双氯芬酸(diclofenac)的三种主要代谢产物中61,有两个与 \(f^-\) 的极大值位置相符,而第三个则位于两个极大值之间的区域(图3)。
洛沙坦(losartan)最重要的代谢产物为 E-317462,其由 CH₂OH 基团氧化为相应的羧酸形成。这一过程与该基团附近 \(f^-\) 的极大值位置一致。然而,在文献9中还报道了另外两种氧化反应——丁基侧链的羟基化。在这两种反应中,仅有一种对应于 \(f^-\) 上一个微小的极大值。
在本研究的药物中,紫杉醇(taxol)的体积最大。对于该分子,所有已报道的代谢产物63均未对应于 \(f^{-}\) 的主要极大值。考虑到如此大尺寸的分子几乎不可能在细胞色素的活性位点内自由旋转,因此其代谢位点首先由立体位阻限制决定。若假设紫杉醇的代谢受空间可及性控制,并进一步假设其三个苯环具有相似的可及性,则值得注意的是:末端苯环上的羟基化反应确实与 \(f^{-}\) 极低等值线(contour levels)所指示的位置相符;而 \(f^{-}\) 值最低的那个苯环实际上完全未被攻击(数据未显示,详见支持信息)。
对于苯妥英(phenytoin),\(f^{-}\) 函数与实际观察到的代谢产物之间呈现出完美的相关性64。
非洛地平(felodipine)表现出极为丰富的代谢产物谱系65。其中大多数涉及1,4-二氢吡啶环氧化为吡啶环,有时伴随一个酯基的丢失。这一过程在 \(f^{-}\) 分布中得到了良好反映;然而,甲基或酯侧链上的羟基化反应则无法与 \(f^{-}\) 的分布相关联。普拉尼地平(pranidipine)的情况亦然66。
MN-1695 的 \(f^{-}\) 分布为胺基被氧取代提供了清晰的线索,即其中一个或两个胺基可被氧化,生成 1,3,5-三嗪-2,4-二酮或 1,3,5-三嗪-2-酮67。
然而,福井函数无法预测苯环上的羟基化反应。另一个重要的代谢产物是三嗪环3位发生的N-氧化反应。根据福井函数的分析,人们本应预期反应发生在位置1或5。
依托泊苷(etoposide)的福井函数在其双甲氧基苯基部分显示出最显著的极大值。实际上,主要代谢产物正是在该区域通过进攻形成的:去甲基化以及氧化生成邻苯醌68。
Δ⁸-四氢大麻酚(Δ⁸-tetrahydrocannabinol)的羟基化产物均源于甲基上的进攻。实验上并未观察到与 \(f^{-}\) 函数预测位置相对应的代谢产物69。
S-MTTPPA70转化为二氢-5-氧代-2-噻吩基化合物的过程可与 \( f^- \) 值较好地相关联。然而,再次强调,在 \( f^- \) 函数中并未显示出对噻吩环上甲基发生羟基化的强烈提示,而事实上该甲基在体内确实会发生羟基化反应70。4-羟基氟比洛芬是氟比洛芬最主要的代谢产物71。福井函数虽提示了其他可能的代谢位点,但这些位点尚未在实验中被观察到。
由于类固醇通常具有高度特异性的代谢特征4,人们本不应期望其代谢攻击位点与任何特定的反应性描述符之间存在明确关联。事实上,基于配体的反应性描述符与实际观测到的代谢产物之间并无相关性。
令人意外的是,对于雌二醇-3-甲醚和地塞米松而言,其主要代谢产物9,11可与 \( f^- \) 的极大值相对应。然而,对于地塞米松的另一主要代谢产物——即饱和六元环上的氧化反应,其对应的福井函数中却未出现明显的极大值。
塞来昔布(Celecoxib)会发生甲基羟基化反应72。尽管在该基团附近存在 \( f^- \) 的极大值,但并无明确的提示信号。值得注意的是,塞来昔布是细胞色素P450酶的抑制剂,因此本文所基于的基本假设(“各向同性反应性”)并不成立。
苯丙香豆素(Phenprocoumon)和华法林(Warfarin)同样可抑制细胞色素P450酶。依据对塞来昔布的分析逻辑,预期其代谢产物与实际观测结果之间应无相关性,或仅有较弱的相关性。然而令人意外的是,所有已观测到的代谢产物均对应于 \( f^- \) 的极大值73。
针对苯丙香豆素计算了两种互变异构体。如图3所示的互变异构体在RI-DFT/BP/TZVP/COSMO(ε = 4.0)理论水平下,其能量比另一互变异构体低约17 kcal/mol。有趣的是,在两种互变异构体中,福奎函数的极大值位置基本一致,仅在 \( \mathrm{O}=\mathrm{C}-\mathrm{C}=\mathrm{C}-\mathrm{OH} \) 结构单元处存在差异(结果未显示)。
所研究的三种化合物为羧酸类(S-MTTPA、氟比洛芬和双氯芬酸)。在生理条件下,这些化合物很可能发生去质子化。此外,已有研究表明,部分细胞色素P450酶能够有效识别并结合阴离子4。图4展示了这些阴离子的 \( f^- \) 函数分布。正如预期,亲电福奎函数的极值主要集中于羧酸根(carboxylate)基团,几乎忽略了分子其余部分的影响。因此,将此类函数与实际代谢产物进行比较并无实际意义。
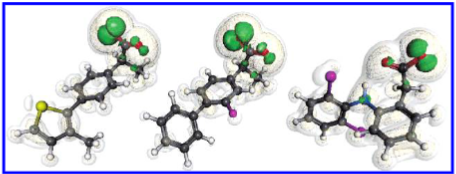
图4. 亲电型福井函数 \(f^{-} \)(左侧)针对酸性化合物 S-MTPPA、氟比洛芬和双氯芬酸的去质子化形式计算所得。参见图3。等值线水平:0.005(绿色,不透明)、0.001(黄色,网状)、0.0005(白色,透明)。
农用化学品
对于农用化学品,大多数代谢研究均在体内进行;仅有少数体外研究被报道,且已证实其中涉及CYP450酶的参与。以下将从四个典型例子展开讨论:氯吡硫磷(chlorpyrifos)、丙嗪(propazine)、对硫磷(parathion)和噻苯咪唑(thiabendazole)74–76。同样,此处仅提供福奎函数的示意图(图5a–d)。
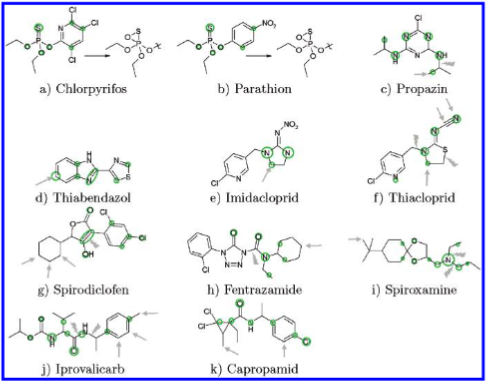
图5. 11个农用化学品的亲电型福井函数 \(f^{-}\) 示意图。灰色箭头表示代谢羟基化的位点;对于非羟基化反应,这些位点或明确标出,或以灰色圆圈表示。灰色“闪电”符号代表键的断裂。绿色圆圈表示 \(f^{-}\) 函数的极大值位置。详见正文。
在人肝微粒体中的体外代谢研究显示,氯吡硫磷和对硫磷的主要代谢途径为对P=S双键的氧化攻击77,该反应位点恰好对应于 \( f^- \) 函数中最为显著的极大值区域。
丙嗪(Propazine)在哺乳动物肝细胞色素P450酶的作用下,其异丙基团发生羟基化,并伴随一个或两个异丙基团的断裂75,这一代谢过程与 \( f^- \) 函数的分布高度吻合。
在哺乳动物细胞中,细胞色素P450酶对噻苯咪唑(thiabendazole)的羟基化反应恰好发生在福奎函数 \( f^- \) 极大值所指示的位置76,与理论预测完全一致。
对于后续的农用化学品——从啶虫脒(imidacloprid)到环丙酰胺(capropamid)(图5e–k),目前尚无体外代谢研究数据。因此,尚不清楚这些代谢过程是否涉及细胞色素P450酶的参与。在此情况下,基于配体的计算方法的一个主要局限性——即忽略酶结构本身——反而可能转化为优势:无论催化生成观察到的代谢产物的是何种酶,该酶通常倾向于攻击底物上热力学上更有利的反应位点(除非底物与酶活性口袋存在特异性结合)。
啶虫脒(imidacloprid)的羟基化反应精确地发生在 \( f^- \) 函数所指示的位置78。类似地,在噻虫啉(thiacloprid)中也观察到了相应的代谢产物79。此外,还检测到腈基(nitrile)的氧化反应;同样,\( f^- \) 函数为这些反应提供了清晰而合理的预测线索。
螺螨酯(Spirodiclofen)含有一个酯基,该基团在植物和动物体内均易发生水解80。因此,未对螺螨酯本身计算其 \( f^- \) 函数,而是针对其水解产物——酮-烯醇互变异构体进行分析。该酮-烯醇的两种互变异构体在RI-DFT/BP/TZVP/COSMO(ε = 4.0)理论水平下的能量差为5.8 kcal/mol,本文仅讨论其中能量更低、热力学更稳定的互变异构体。在动物体内,观察到环己烷环上的羟基化以及酮-烯醇环的氧化开环反应80。尽管 \( f^- \) 函数显示烯醇双键处具有较高的反应活性,但其对脂肪族环结构的显著活化特征却未被清晰体现。
芬特拉酰胺(Fentrazamide)的 \( f^- \) 函数提示在脂肪族位点可能发生攻击,然而这些位点在体内并未观察到实际代谢产物81。相反,实际检测到的代谢物也未能与任何 \( f^- \) 极大值相对应。
螺氧咪胺(Spiroxamine)中的叔胺基团可发生N-氧化、连接氮原子的脂肪链羟基化以及胺侧链降解82,这些反应路径均与 \( f^- \) 函数所预测的活性位点一致。然而,对叔丁基(tert-butyl)基团的羟基化反应却无法通过直接观察 \( f^- \) 函数进行合理预判。
异丙噻菌胺(Iprovalicarb)是一种高度柔性的分子,其 \( f^- \) 极大值的位置在很大程度上与分子构象无关。酰胺基团的 \( f^- \) 值显著高于O-C(=O)-NH基团,尤其是在羰基氧原子处表现出更高的反应活性。事实上,实验观察到的键断裂主要发生在酰胺键上83。然而,甲苯基(toluyl)片段的羟基化位点却无法与任何显著的 \( f^- \) 极大值相对应。
类似地,环丙酰胺(capropamid)的 \( f^- \) 函数与其实际观察到的代谢产物之间也缺乏明确关联84。尽管在氯原子邻位的苯环上存在一个微弱的 \( f^- \) 极大值,对应于该位置的羟基化反应,但这一信号极小,极易被忽略。此外,对于甲基的羟基化反应,\( f^- \) 函数完全未提供任何可识别的提示。
综上所述,仅依赖 \( f^- \) 极大值难以作为预测药物或农用化学品代谢攻击位点的可靠工具。代谢反应过程远比想象中复杂,该方法尤其忽视了脂肪族侧链上的羟基化反应。相比之下,芳香环中心的羟基化以及其他反应(如N-氧化、键断裂等)往往与 \( f^- \) 极大值位置吻合较好。另一方面,基于半经验方法估算氢原子攫取能10,11虽在脂肪族侧链的预测上似乎未表现出类似缺陷,但此类计算亟需重新参数化,以实现芳香环与脂肪族位点氧化反应之间的合理平衡。当然,诸如N-氧化等反应也无法通过氢原子拔氢反应能来准确预测。
分子对接(docking)方法在预测细胞色素P450介导的羟基化反应方面已取得相当成功(例如参见文献9)。正如Zamora等人在本文中指出,该方法完全未考虑局部反应性因素,而这很可能正是其主要误差来源之一。因此,分子对接与本研究的方法——即忽略蛋白质特异性相互作用——具有很强的互补性。将分子对接与局部反应性描述符相结合,或可成为QM/MM模拟代谢反应路径的一种可行替代方案。有理由相信,这种整合策略有望在计算成本相对较低的前提下实现足够的预测可靠性,从而支持中等通量的代谢位点预测研究。
细胞色素P450
图6a、b所示的自旋密度 \( \Delta \rho \) 表明,自由基态在很大程度上局域于铁原子及其配位氧原子附近。在双线态(doublet)中,这种局域化现象更为显著;而在四线态(quartet)中,部分自旋密度则分布在硫原子附近,并在整个自旋密度分布轮廓上呈现较广的分散特征。这一定性趋势与近期更精确的量子力学/分子力学(QM/MM)研究结果一致5,15。基于此,我得出结论:采用RI-DFT方法对血红素核心及少数嵌入介电连续介质中的氨基酸残基进行计算,足以获得合理的电子密度分布。
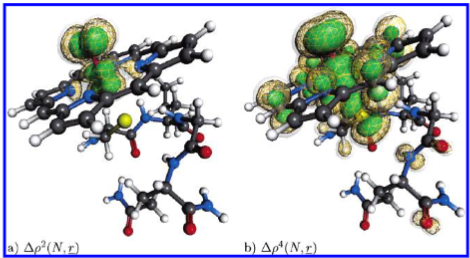
图6. 复合物I(Cpd I)模型体系的(a)双重态和(b)四重态的自旋密度分布。等值线水平:0.005(绿色,不透明)、0.001(黄色,网状)、0.0005(白色,透明)。符号标注见式12。详见正文。
对福井函数(Fukui functions)的分析(见图7)表明,由四线态氧密度 \( \rho^4(N_r) \) 推导出的反应性在与铁原子相连的氧原子位置上并未表现出任何显著极大值。\( f_{4,4}^+ \) 紧密局域于铁原子周围;同样地,\( f_{4,4}^- \) 的中心极大值也主要位于吡咯氮原子处。而由双线态密度 \( \rho^2(N_r) \) 推导出的福井函数 \( f_{2,4}^+ \) 与 \( f_{2,4}^- \) 则高度局域于Fe–O基团中的氧原子上。这两类函数均在氧原子的p轨道以及铁原子的d轨道处表现出明确的极大值。毫不意外的是,\( f_{2,4}^- \) 的分布与图6中双线态的自旋密度 \( \Delta \rho^2 \) 高度吻合。
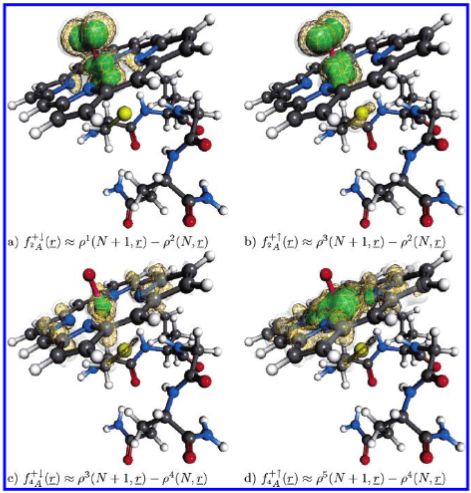
图7. 复合物I(Cpd I)模型体系的亲核型福井函数。图a和b显示由双态产生的 \( f^{+} \) 函数;图c和d分别为由四重态产生的相应函数。符号标注遵循式11。详见正文。
从福井函数的分析可得出结论:相较于四线态,双线态在Fe–O氧原子位置表现出更强的局部反应活性。在文献12和13中亦发现,与四线态相比,双线态通过反弹机制(rebound mechanism)进行氧化的路径具有略微更优的热力学能势。本文所获得的定性结果与此一致,进一步支持了双线态在该反应体系中可能更具反应活性的观点。
结论
已对18种药物和11种农用化学品计算了亲电性福井函数(f⁻)。仅有两种药物和两种农用化学品未能建立该函数最大值与观察到的代谢反应之间的关联。对于其余化合物,理论与实验结果之间确实存在一致性。然而,在脂肪族碳原子上的代谢反应是一个著名的例外情况:很少能将所有代谢攻击位点都归因于福井函数的最大值。
福井函数不应被视为预测代谢途径的手段。更准确地说,这些函数无法帮助预测可能发生何种类型的反应。然而,若与具有丰富经验的代谢专家(尤其是(分子)生物学家)密切合作,这一理论概念或许有助于指导代谢产物的搜寻工作,特别是当福井函数“局域化”(即聚焦于分子的某些特定区域)时。
这种基于配体的方法的根本弱点——忽略酶特异性相互作用——也可被视为其优势。代谢反应不仅限于细胞色素介导的氧化反应,也不仅限于亲电攻击。因此,福井函数(f⁻ 以及 f⁺)有助于理解那些酶源未知的体内代谢反应。这一点已在七种农用化学品中的五种中得到验证,这些化合物此前并无体外实验数据。
针对Cpd I模型体系计算得到的亲核性福井函数,在定性上与复杂的量子力学/分子力学(QM/MM)结果相符。这一结果令人鼓舞,因为它可能激励进一步开展代谢反应预测的研究工作。对于此类研究,结合分子对接与局部反应性的方法,虽然可靠性略低于对完整反应路径进行的QM/MM计算,但成本显著更低,是一种极具潜力的替代方案。
文献
略
如何计算福井函数
原创文章,作者:小墨,如若转载,请注明出处:《福井函数极大值与代谢位点相对应吗?》http://blog.molcalx.com.cn/2025/09/07/do-fukui-function-maxima-relate-to-sites-of-metabolism.html



