摘要：本文以西地那非的一个片段为例，演示了如何用Numpy来求解原子所在面、法线以及点到面距离。更具体地讲，本文以杂环芳香性计算为场景，演示了如何借助Flare的原子选择与内置的Numpy来计算NICS(0)与NICS(1)虚原子坐标，创建NICS计算文件。总的来说，借助Flare及其内置的Numpy，可以方便帮助我们进行NICS计算以确定感兴趣片段的芳香性，为生物等排体替换提供决策支持。

肖高铿/2022-01-16

问题的起源

在芳香性基团生物等排体替换的项目中我们需要确保新的片段也具有芳香性，NICS是简单、高效、且可靠的计算方法[1]。比如辉瑞公司Tu等人[2]提出的芳环生物等排替换方法NEAT正是采用NICS法来判断候选片段的芳香性。鉴于NICS(0)与NICS(1)是最常用的芳香性指标，我们详细描述了如何利用Gaussian来计算NICS(0)与NICS(1)[3]，其中关键的步骤之一是确定NICS(0)与NICS(1)虚原子的空间坐标。

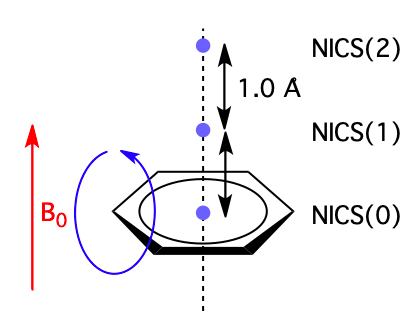
NICS示意图

图1. NICS计算示意图

如图1所示，为了计算NICS(0)与NICS(1)，首先需要确定这两点的坐标。其中NICS(0)为感兴趣环的几何中心（不是质心），而NICS(1)为从环上重原子几何中心处沿着垂直于平面方向移动1Å距离处的点。如图2所示，在前文中[4]我们以西地那非的一个杂环片段为例已经演示过如何获得NICS(0)点的坐标，本文的目的是演示如何获得NICS(1)点的坐标并进行NICS计算。

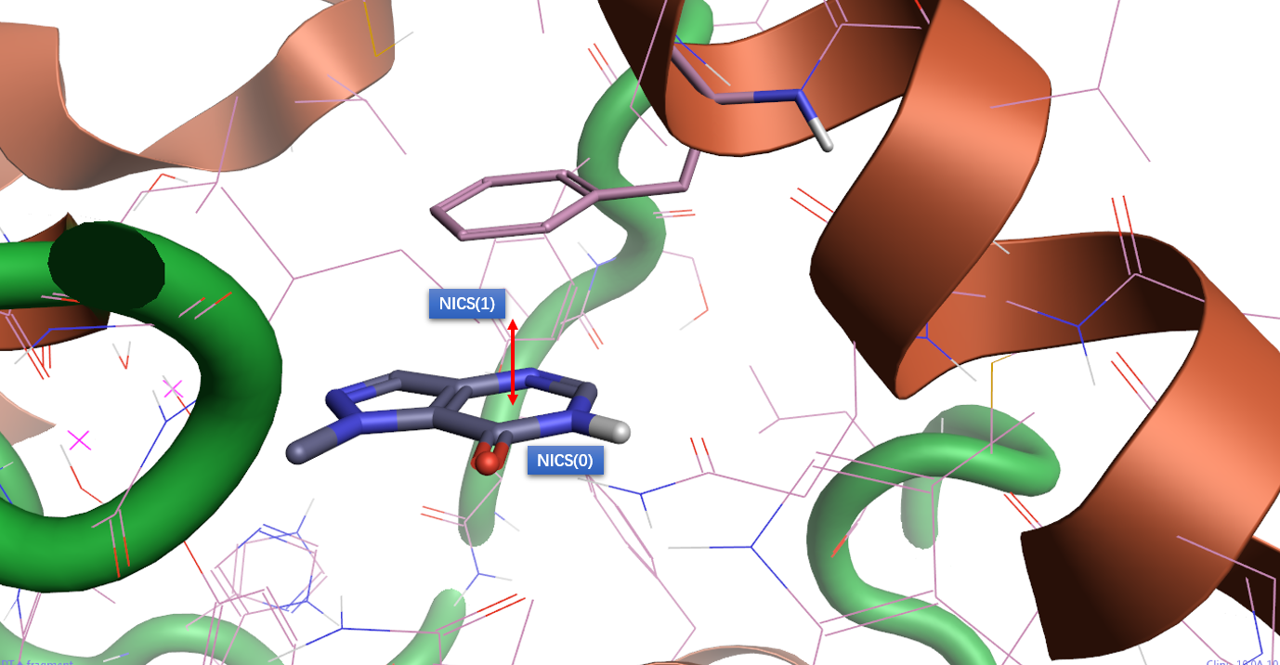
NCIS芳香性计算

图2. NICS算例说明。以PBD 1UDT配体西地那非的一个杂环母核为例，以六员杂环几何中心为NICS(0)点，需要将穿过该点、距离六员环平面1Å处的坐标求出用于NICS(1)计算

思路

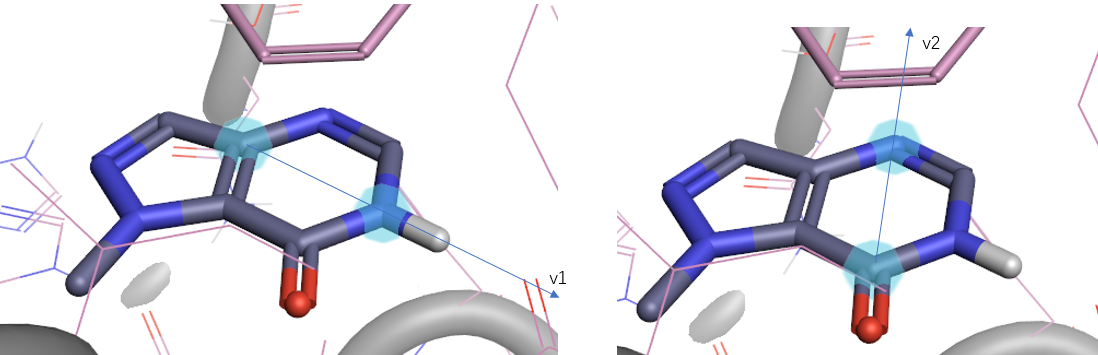
向量v1与v2定义苯环平面

图3. 六员杂环所在平面的确定示意图。两个原子确定一个向量，用v1与v2向量来确定杂环所在的平面。

之前[4]已经讨论过，空间的每个原子坐标都可视为一个向量，六员杂环所在的平面可用其中两发生交叉的向量来表示，如图3所示。那么我们的问题可以简化为求解穿过平面上点M且距离平面为1Å的点N的坐标，如图4所示。

solution

图4. 穿过v1与v2所在平面点M且到平面的距离为1Å的点N。

其中点M的坐标已知，我们在上一次已经求解出来[4]。现在只需要求解点N即可。如果点M用向量c0表示，其法向量为n0，那么穿过点M且距离平面为d的点有两个，分别为：

c0+d*n0或c0-d*n0

只要计算出n0并代入上式即可得到点N的坐标。

操作步骤

最后两行的输出，就是两个NICS(1)的坐标：

1
2

1.15640274 64.02874937 84.93070186
-0.32240276 65.37524869 84.93929834

接下来，可以用Guassian开始NICS计算了。

NICS计算

将上面计算得到杂环中心(点M)与两个点N（只需要其中一个即可）的坐标作为虚原子，创建Gaussian输入文件：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#p nmr m062x/6-311+g(d,p)
 
 fragment
 
0  1
C           1.30800        65.68400        84.44200
N           1.12500        65.47400        85.81600
C           0.26000        64.51900        86.34600
C          -0.49500        63.70000        85.44000
C          -0.29300        63.92800        84.04600
N           0.59700        64.90700        83.52000
O           0.18000        64.42200        87.54900
N          -1.41400        62.69600        85.61200
N          -1.79800        62.28000        84.37000
C          -1.11400        63.03100        83.40500
C          -1.94800        62.11100        86.84500
H          -2.67200        61.32200        86.59400
H          -1.12400        61.67900        87.43200
H          -2.44800        62.89300        87.43500
H           1.64600        66.04300        86.45300
H           1.93790        66.37920        84.12160
H          -1.20790        62.93140        82.41440
Bq         0.417000        64.70200        84.93500 
Bq         -0.32240        65.37525        84.93930
 
! blank line

其中第23行虚原子代表杂环中心点M，第24行虚原子代表点N。用GaussView 6进行可视化，结果如图5所示。

NICS计算

图5. GaussView对输入文件进行可视化检查，可以看到两个紫色的点，即为虚原子。其中一个在杂环中心为NICS（0）坐标，另一个在环外，为NICS（1）坐标。

用GaussView对输入文件进行可视化检查，可以看到两个紫色的点，即为虚原子。其中一个在杂环中心为NICS（0）坐标，另一个在环外，为NICS（1）坐标。我们可以发现，确实计算出来的坐标如预想的那样穿过六员杂环的几何中心点M，并得到正确的点N坐标。

NICS计算结果如下:

1
2
3
4
5
6
7
8
9
10

     18  Bq   Isotropic =     3.2688   Anisotropy =    14.2286
   XX=    -0.0365   YX=    10.1102   ZX=     5.7735
   XY=     6.7677   YY=     1.6117   ZY=    -0.3916
   XZ=     3.9496   YZ=     1.7013   ZZ=     8.2310
   Eigenvalues:    -8.3255     5.3773    12.7545
     19  Bq   Isotropic =     5.8319   Anisotropy =    11.2832
   XX=     6.2029   YX=    -1.5203   ZX=     6.4919
   XY=    -6.8056   YY=     5.4782   ZY=    -4.6659
   XZ=     4.0089   YZ=     1.8145   ZZ=     5.8145
   Eigenvalues:    -0.0796     4.2212    13.3540

其中1行第18号虚原子为NICS(0)对应虚原子位置处的各向同性化学位移屏蔽值，第6行第19号虚原子为NICS（1）对应值虚原子位置处的各向同性化学位移屏蔽值。NICS为各向同性化学位移屏蔽值的负值，因此NICS(0)与NICS(1)分别为-3.2688与-5.8319。值越小（越负）则代表所具有的芳香性越强，这说明该六员杂环片段具有芳香性。更多的结果解释请参见文[3]，这里不再细述。

接下来可以做什么

  1. 批量计算

    2. 修改一下代码，批量地计算潜在生物等排体候选片段的芳香性，为您的骨架跃迁提供决策支持。

  2. 可视化分析

    3. 在分子周围设置很多虚原子，进行等值图可视化分析，如图6所示来源自Cleinpeter等人[5]文章的硝酸阴离子与4-甲基吡啶的磁屏蔽效应。

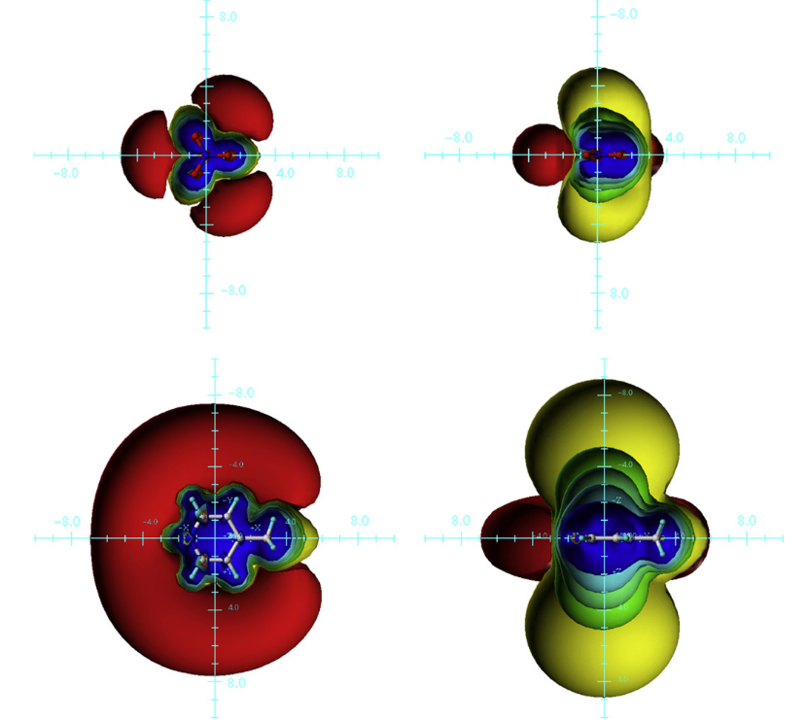
    磁各向异性

    图6. 硝酸根阴离子与4-甲基吡啶的空间NMR屏蔽可视化分析。蓝色代表 ～5 ppm屏蔽；青色，～2 ppm屏蔽；绿蓝色，～1 ppm屏蔽；绿色，～0.5 ppm屏蔽；黄色， ～0.1 ppm 屏蔽；红色，～0.1 ppm去屏蔽）

文献

  1. Schleyer, P. V. R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N. J. R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118 (26), 6317–6318. https://doi.org/10.1021/ja960582d.
  2. Tu, M.; Rai, B. K.; Mathiowetz, A. M.; Didiuk, M.; Pfefferkorn, J. A.; Guzman-Perez, A.; Benbow, J.; Guimarães, C. R. W.; Mente, S.; Hayward, M. M.; et al. Exploring Aromatic Chemical Space with NEAT: Novel and Electronically Equivalent Aromatic Template. J. Chem. Inf. Model. 2012, 52 (5), 1114–1123. https://doi.org/10.1021/ci300031s.
  3. 陈宇. 计算NICS值评估分子体系的芳香性和反芳香性. 墨灵格的博客. 2021-01-09. http://blog.molcalx.com.cn/2021/01/09/calculate-nics-to-evaluate-aromaticity.html
  4. 肖高铿. 在Flare里计算两个环的几何中心及其之间的距离. 墨灵格的博客. 2022-01-15. http://blog.molcalx.com.cn/2022/01/15/center-and-distance.html
  5. Kleinpeter, E.; Koch, A.; Sahoo, H. S.; Chand, D. K. Anisotropic Effect of the Nitrate Anion-Manifestation of Diamagnetic Proton Chemical Shifts in the 1H NMR Spectra of NO3- Coordinated Complexes. Tetrahedron 2008, 64 (22), 5044–5050. https://doi.org/10.1016/j.tet.2008.03.063.

联系我们，获取免费试用1个月的Flare