摘要：根据Grayson等人的研究结论：活化能小于20.7kcal/mol且ELUMO小于-1.85eV的Michael受体很可能就是DNA的直接诱变剂。为了推广该研究成果，本教程详细地描述了如何利用高斯软件搜索Michael受体与碱基模型分子甲胺反应的过渡态、计算反应活化能、计算HOMO与LUMO能量，最后预测化合物的遗传毒性（AMES test）。

作者：陈宇，肖高铿
时间：2020-01-08

关于Michael受体与遗传毒性（AMES test）

此前在介绍Houk课题组关于Michael受体硫醇加成反应的动力学与热力学在共价药物设计中的意义[1,2]的工作时提到过Michael受体是目前靶向CYS残基共价抑制剂设计的主要方式，已经有afatinib、osimertinib与ibrutinib等药物被批准已经上市。在Houk课题组的研究中，还详细描述了如何用DFT理论计算预测一个Michael受体能否与半胱氨酸巯基发生可逆共价结合。

然而，Michael受体的共价结合能力也带来一定潜在的遗传毒性(致突变性)风险，因此有必要对其进行充分的评估。AMES试验是一种广泛的遗传毒性(致突变性)生物测定方法，传统的AMES测试预测方法往往基于化学结构，由于其忽略了与DNA反应性有关的内在化学过程，因此预测结果很可能导致假阳性。Grayson等人[3]报道了一种基于DFT的有效AMES测试预测方法，仅仅通过对模型碱基与Michael受体的反应活化能以及Michael受体的LUMO能量进行计算，就能够有效的评估Michael受体的致突变性，详细见博文：《用DFT预测1,4-Michael受体的AMES致突变性》[4]。

本教程的目的是为了推广Grayson等人的研究成果，选了4个Michael受体（图1）并用甲胺作为碱基模型，计算了四个化合物Michael加成反应过程的能垒和四个Michael受体的LUMO能量，主要目的是回顾反应能垒和HOMO/LUMO能量的计算流程。

Gaussian教程 | 用DFT预测Michael受体的遗传毒性(AMES test)-墨灵格的博客

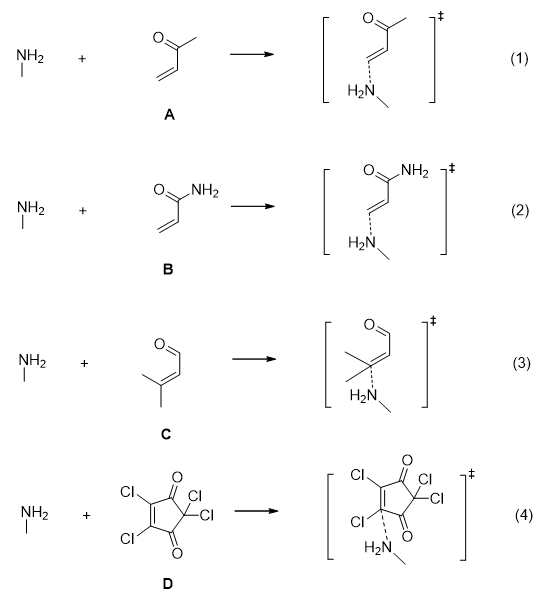
图1. 4个Michael受体化合物

操作步骤

以反应式（1）为例，详细介绍如何进行过渡态的搜索、计算活化能以及Michael受体A的HOMO/LUMO能量。其中过渡态的成功搜索依赖于能够构建一个合理的过渡态结构的初始猜测，许多方法能够达到这一目的，在这里我们为寻找简单体系的过渡态提供一个简单通用的流程。

1. 优化参与反应的Michael受体A

Michael受体A的优化输入文件如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

%nprocshared=24
%mem=12GB
# b3lyp/def2tzvpp opt freq scrf=(iefpcm,solvent=water) em=gd3bj
 
A
 
0 1
 C                 -1.92297691    2.08585029   -0.15603324
 O                 -0.69565991    2.08585029   -0.15603324
 C                 -2.74417305    0.78306984   -0.15597916
 H                 -2.24367707   -0.16265939   -0.15593991
 C                 -4.09854918    0.83031772   -0.15598112
 H                 -4.60465528    1.77305660   -0.15602025
 H                 -4.66373243   -0.07823491   -0.15594341
 C                 -2.74417305    3.38863074   -0.15603324
 H                 -3.34161750    3.43364762   -1.04256221
 H                 -3.38022845    3.40930955    0.70414459
 H                 -2.08124425    4.22811334   -0.12968211
 
!空白行为特意留出，不可忽略

其中第3行scrf=(iefpcm,solvent=water)指示程序在计算中考虑溶剂化（水）作用; em=gd3bj为泛函添加色散校正。

计算完毕，可以在结果文件里找到如下的字段，我们关心第8行的自由能（即后面会用到的GA）。

1
2
3
4
5
6
7
8

 Zero-point correction=                           0.089369 (Hartree/Particle)
 Thermal correction to Energy=                    0.095134
 Thermal correction to Enthalpy=                  0.096078
 Thermal correction to Gibbs Free Energy=         0.060515
 Sum of electronic and zero-point Energies=           -231.265337
 Sum of electronic and thermal Energies=              -231.259572
 Sum of electronic and thermal Enthalpies=            -231.258628
 Sum of electronic and thermal Free Energies=         -231.294191

2. 优化参与反应的甲胺分子

甲胺分子优化的输入文件如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

%mem=12GB
%nproc=8
# b3lyp/def2tzvpp em=GD3BJ scrf=(iefpcm,solvent=water) opt freq
 
NH2Me
 
0 1
 C                 -2.01773996    0.22874732    0.34396808
 H                 -2.38526785   -0.73690804    0.62205613
 H                 -2.35424492    0.95617178    1.05285317
 H                 -2.38349391    0.48299280   -0.62890564
 N                 -0.54803226    0.20674602    0.32459779
 H                 -0.23354164   -0.47308937   -0.33791220
 H                 -0.20454824    1.10922789    0.06470316
 
!空白行为特意留出，不可忽略

计算完毕，可以在结果文件里找到如下的字段，我们关心第8行的自由能（即后面会用到的GCH3NH2）。

1
2
3
4
5
6
7
8

 Zero-point correction=                           0.063783 (Hartree/Particle)
 Thermal correction to Energy=                    0.067218
 Thermal correction to Enthalpy=                  0.068162
 Thermal correction to Gibbs Free Energy=         0.040846
 Sum of electronic and zero-point Energies=            -95.849065
 Sum of electronic and thermal Energies=               -95.845630
 Sum of electronic and thermal Enthalpies=             -95.844686
 Sum of electronic and thermal Free Energies=          -95.872002

3.构建过渡态结构的初始猜测

首先，将优化好的两个反应物分子复制到GaussView 6的同一个分子构建界面中；然后把在过渡态中将要成键的两个原子用虚键连接起来（图2）；接下来点击‘Clean’工具（图2），分子会根据经验参数调整自身结构，对于比较简单的过渡态结构，这种方法通常有效。

Gaussian教程 | 用DFT预测Michael受体的遗传毒性(AMES test)-墨灵格的博客

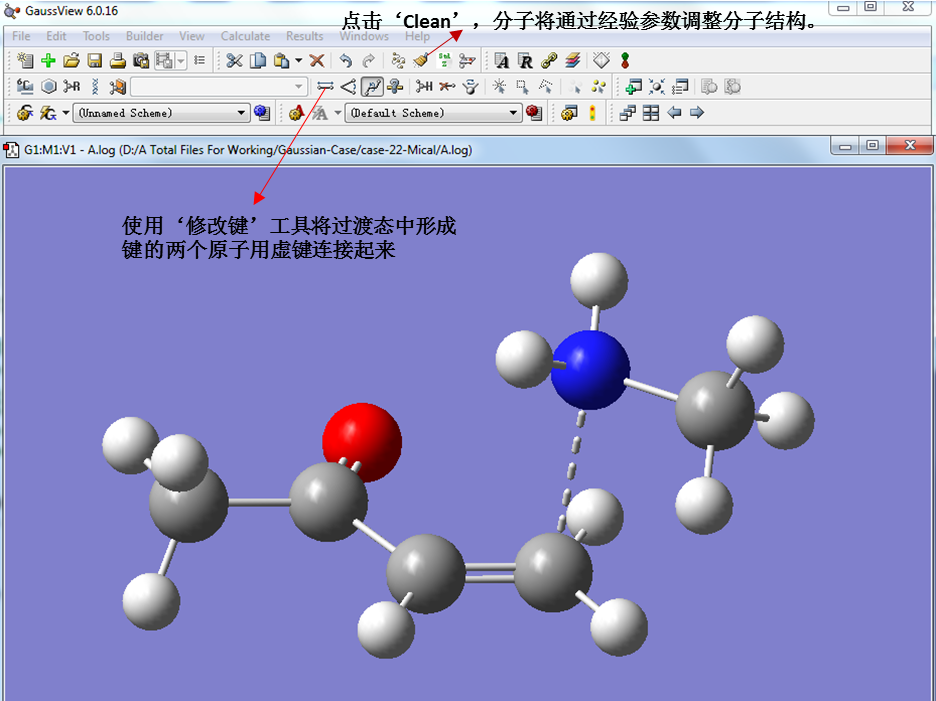
图2. 构建过渡态结构的初始猜测

接下来，保存好结构，编辑输入文件，即可提交文件开始过渡态的寻找，很幸运！在我们的例子中，只进行了一次初始构型猜测便得到了过渡态结构。对于更复杂的过渡态结构，我们可能很难一次得到过渡态结构，这时需要根据失败的结果调整初始构型，使其更靠近真实的过渡态结构，以增大成功的概率。

最后准备好的过渡态优化的输入文件如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

%nprocshared=24
%mem=12GB
# b3lyp/def2tzvpp opt=(ts,calcfc,noeigen) freq scrf=(iefpcm,solvent=water) em=gd3bj
 
opt
 
0 1
 C                 -2.06709983    2.60157584   -0.29598028
 O                 -0.81008518    2.63541798   -0.34434796
 C                 -2.79237615    1.26627164   -0.04590637
 H                 -3.86119827    1.23749583   -0.00478189
 C                 -2.07691114    0.12764973    0.12207279
 H                 -1.03251684    0.34866392    0.04931788
 H                 -2.34587348   -0.57773259   -0.63621149
 C                 -1.26877679   -0.80292334    2.89060627
 H                 -0.56352336   -1.42550225    2.38078954
 H                 -0.85945739    0.17888054    3.00644564
 H                 -1.47931238   -1.21755569    3.85427363
 N                 -2.51077187   -0.72680292    2.10794805
 H                 -2.89331336   -1.64437665    1.99968695
 H                 -3.16988722   -0.14495348    2.58441228
 C                 -2.88012815    3.89546484   -0.48686298
 H                 -3.64183403    3.73310432   -1.22058174
 H                 -3.33302255    4.17244610    0.44215158
 H                 -2.23042390    4.67984454   -0.81478502
 
!空白行为特意留出，不可忽略

4. 检查优化的结构是否为需要的过渡态结构

首先查看是否只有一个虚频，如果只有一个虚频，说明优化的结构是一个过渡态结构，但这并不保证是我们想要的过渡态结构，因此需要进行一个IRC计算，以此来确定这个过渡态连接反应物和产物。

关于IRC详细的计算过程请参考：Gaussian教程 | 搜索过渡态[5]。

5. 提取自由能信息

当我们优化完所有的结构后，需要构建反应势能面，这其中就包含了反应活化能的信息。由于我构建的是反应自由能面，因此我们需要提取每个分子的自由能信息。我们以A分子-甲胺的过渡态为例，用文本编辑器打开Gaussian计算结果log文件，找到下面的字段(Sum of electronic and thermal Free Energies），第8行给出了自由能（即后面会用到的G‡）。

1
2
3
4
5
6
7
8

 Zero-point correction=                           0.156394 (Hartree/Particle)
 Thermal correction to Energy=                    0.165563
 Thermal correction to Enthalpy=                  0.166507
 Thermal correction to Gibbs Free Energy=         0.121366
 Sum of electronic and zero-point Energies=           -327.098888
 Sum of electronic and thermal Energies=              -327.089719
 Sum of electronic and thermal Enthalpies=            -327.088775
 Sum of electronic and thermal Free Energies=         -327.133916

6. 读取Michael受体的HOMO与LUMO能量

GaussView 6| File | Open打开分子A结构优化的结果文件（A.log文件）, 点击GaussView 6菜单的MO编辑器（图3）。

Gaussian教程 | 用DFT预测Michael受体的遗传毒性(AMES test)-墨灵格的博客

图3.MO编辑器

在弹出的MO编辑器里，可以直接读取HOMO与LUMO的能量（图4）。

Gaussian教程 | 用DFT预测Michael受体的遗传毒性(AMES test)-墨灵格的博客

图4.HOMO与LUMO轨道能量

上图中19号轨道为HOMO轨道，对应的能量即为HOMO轨道能量；20号轨道是LUMO轨道，对应的能量为LUMO轨道能量。需要注意的是，此能量单位Hartree，通常轨道能量需要换算成eV，其换算公式为：

1 Hartree = 27.21 eV = 627.5 kcal/mol

7. 结果分析

Michael A与碱基模型分子甲胺反应的活化能(反应能垒)根据下式计算：

Reaction Energy Barrier, ΔG = G‡ - (GA + GCH3NH2)

= -327.133916-(-95.872002-231.294191) Hartree

= 20.3 kcal/mol

利用同样的方法我们计算出了4个Michael受体与碱基模型的反应能垒和Michael受体的HOMO/LUMO能量，并列于表1中。

表1. 4个Michael受体与碱基模型的反应能垒及其HOMO与LUMO能量

Michael受体 A B C D
活化能(kcal/mol) 20.3 26.8 24.1 15.1
EHOMO（eV） -1.95 -1.41 -1.83 -3.65
ELUMO（eV） -7.3 -7.48 -7.2 -8.09


根据Grayson等人结论：活化能小于20.7kcal/mol且ELUMO小于-1.85eV的Michael受体很可能就是DNA的直接诱变剂。因此可以预测化合物A、D为AMES test阳性化合物，而B、C为AMES test阴性化合物。这个预测与实验结果一致，重现了Grayson等人的结果。

注意事项

1.在方法基组选择合适的情况下，活化能计算的准确性严格依赖于构象的选择，因此得到能量最低的构象非常关键，如果构象不合适，甚至会得出错误的结论。

2.我们的计算并不是完全重复原文中的数据，但这并不影响得出最终的结论。原文对自由能进行了温度，浓度和频率的校正。然而需要说明的是校正方法通常源于经验，甚至不同的文献校正参数也不同，因此需要谨慎使用。

文献

  1. Krenske, E. H., Petter, R. C., & Houk, K. N. (2016). Kinetics and Thermodynamics of Reversible Thiol Additions to Mono- and Diactivated Michael Acceptors: Implications for the Design of Drugs That Bind Covalently to Cysteines. The Journal of Organic Chemistry, 81(23), 11726–11733
  2. 可逆Michael受体硫醇加成反应的DFT理论计算. http://blog.molcalx.com.cn/2020/01/04/thiol-addition-to-michael-acceptor.html
  3. Townsend, P. A.; Grayson, M. N. Density Functional Theory Transition-State Modeling for the Prediction of Ames Mutagenicity in 1,4 Michael Acceptors. J. Chem. Inf. Model. 2019, acs.jcim.9b00966
  4. 用DFT预测1,4-Michael受体的AMES致突变性. http://blog.molcalx.com.cn/2019/12/12/use-dft-to-predict-the-ames-mutagenicity-for-michael-acceptor.html
  5. Gaussian教程 | 搜索过渡态. http://blog.molcalx.com.cn/2017/11/18/gaussian-tutorial-transition-state.html

联系我们