用张力能评估构象稳定性及其在先导化合物优化中的应用——更多力场选择
摘要:本文用两对化学结构仅一个原子差异但活性相差巨大的分子对为例,尝试用FreeForm以不同的力场计算张力能来解释活性差异的原因。第1个算例来自JAK3共价抑制剂,化合物具有活性与非活性两种潜在构象,freeform可以正确地对活性与非活性构象的张力能进行排序,并解释活性差异的原因。第2个算例为一对溴代与脱溴的PTP1B抑制剂,其活性差异主要源于Br的立体位阻,freeform的张力能可以正确地对这一对化合物的活性进行排序,并解释活性差异原因,这可以弥补分子对接打分函数与相互作用分析的不足。在两个算例中,不管用哪个力场,都对化合物的张力能做出了正确判断。不同力场计算的张力能在数值上差异也相当大,需要更多的算例进行验证哪个力场更好、更具普适性。无论如何,FreeForm提供了多种的力场选择以应对不同的场景。
肖高铿/2022-02-07
1. 用张力能(Strain energy)评估构象稳定性
化合物结合构象稳定性常用化合物的张力能(Strain Energy)来评价:通常以全局最低能构象为参比,以构象的相对能量值来计算张力能以评估构象稳定性,如图1所示。
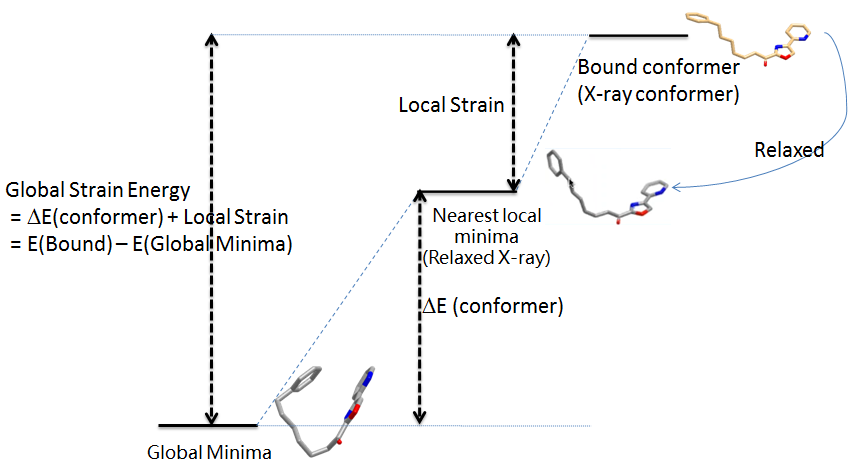
图1. 传统的Strain Energy计算方法:以全局极小构象为参比。
这种张力能计算方法存在很明显的问题:只考虑了活性构象与全局极小点,忽略了熵的贡献。配体分子与靶标结合时真实过程是:在溶剂中从非结合的构象系综变为在蛋白结合口袋中单一的生物活性构象,如图2所示。
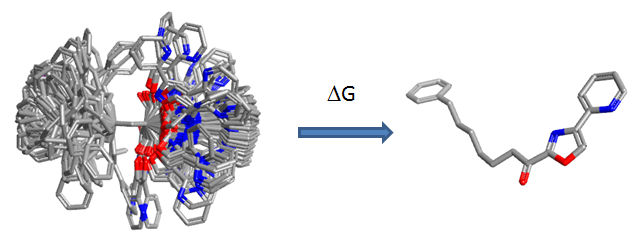
图2,配体分子与靶标结合的构象变化:由在溶剂中的非结合构象系综变为在结合口袋中的单一生物活性构象
传统的张力能虽然直观且容易凭经验即可对不同构象进行比较,但上述的缺陷常常导致不能正确评估构象的稳定性。因此我们需要一个更合适的张力能计算方法。Freeform是OpenEye药物设计软件包的一个应用,可以用来计算化合物的溶剂化自由能以及计算化合物从一个构象系综变为一个单一生物活性构象或其它单一构象的自由能变化,原理如图3所示。
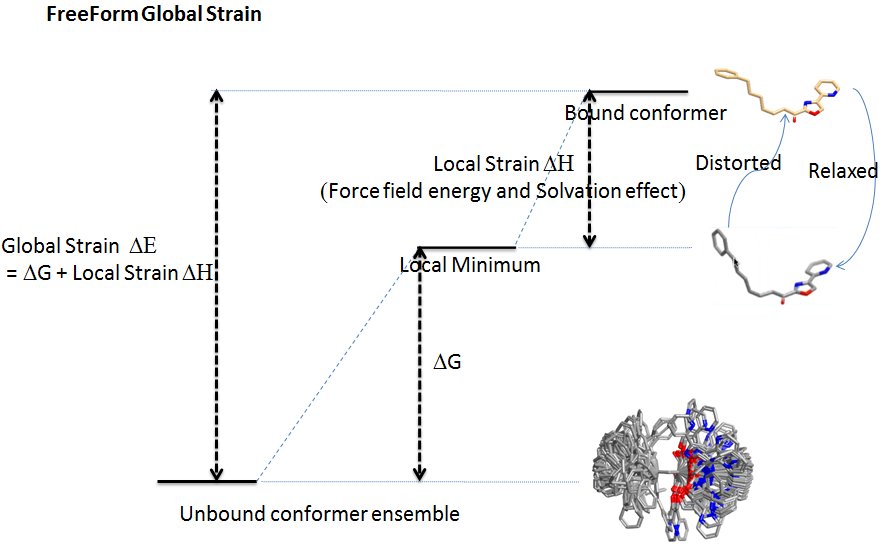
图3,FreeForm重新定义了张力能:不仅以配体非结合状态的构象系综为参比,还考虑了主要的熵成分,其张力能采用构象自由能来计算
由于配体的结合构象可能不是极小点,因此不能用sum-of-states来直接计算自由能。FreeForm将结合构象的张力能可以拆解为两部分:1)结合构象附近极小点的构象自由能(Relaxed Bioactive ΔG);与2)极小点与结合构象的焓变(Local ΔH)。活性构象的全局张力能(Global ΔE)则表示为:
Global ΔE = Relaxed Bioactive ΔG + Local ΔH
准确的张力能计算非常重要,此前我已经介绍过FreeForm张力能计算在构象约束策略实现先导化合物优化中的应用[1],尤其适用于大环分子的设计;还介绍过如何用FreeForm联合MM/PBSA使用来改善MM/PBSA计算精度以便更好地对化合物排序[2]。本文的主要目的之一是演示如何用张力能来理解先导化合物优化过程中的SAR,尤其是修饰一个原子而引起活性巨大变化的场景。本文的另一个目的是尝试使用新引入的Open Force Field,并与模型的MMFF94S力场计算结果进行比较。
2. 算例1:JAK3共价抑制剂
2.1 算例介绍
辉瑞公司开发选择性JAK3共价抑制PF-06651600的灵感来源于托法替尼(Tofatinib)与JAK3的共晶结构(PDB 3LXK)[3,4]:如图4所示,围绕嘧啶胺N-C键旋转可能会使侧链的酰胺取代基紧邻CYS909,适当设计的亲电试剂可以捕获到亲核的半胱氨酸。
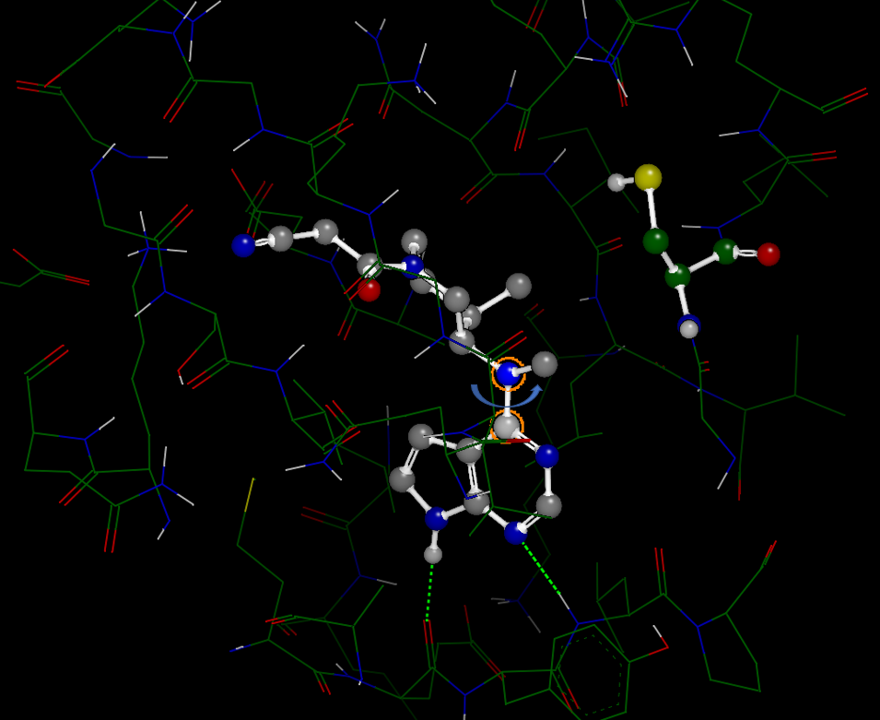
图4. 托法替尼与JAK3的共晶结构(PDB 3LXK)。腈基处于远离CYS909的一端,围绕嘧啶胺N-C键(高亮部分)旋转可能会使侧链的酰胺取代基紧邻CYS909
那么将丙烯酰胺安放在托法替尼母核上就可能得到共价抑制剂。下面为了讨论方便,将丙烯酰胺取向与托法替尼腈基取向一致的pose称为非活性构象,因为其远离Cys残基不能与Cys发生加成反应;而将丙烯酰胺片段指向Cys的构象称为活性构象。在探索JAK3靶向CYS的共价抑制剂过程中,发现化合物1、2仅差异一个甲基,但是对JAK3的Ki差异达到69倍,如图5所示。
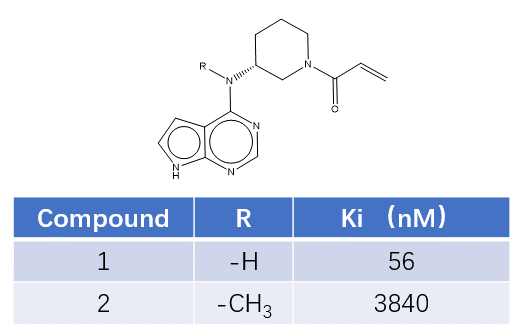
图5. 化合物1、2及其对JAK3的活性
之前,我们已经讨论过化合物1、2活性差异原因[5],基于QM的构象稳定性分析表明:化合物1的活性构象与旋转180°之后的非活性构象相比具有更低的构象能,两者占比大约为70:30;化合物2的活性构象与旋转180°之后的非活性构象相比构象能相似,两者占比大约为50:50;化合物1的Michael受体比化合物2的有更多的机会与Cys发生加成反应。因此用FreeForm对化合物1、2的活性与非活性构象进行分析,可以预期到:化合物1的活性与非活性构象自由能差异要比化合物2的活性与非活性构象自由能差值大。
2.2 结构准备
鉴于化合物1与JAK3的共晶结构已经解释(PDB 5TTS),因此其活性构象可从共晶结构提取,仅对乙烯基片段用力场进行优化后作为化合物1的活性构象;手动对化合物1的C-N进行180度旋转后,作为化合物1的非活性构象。再分别将化合物1的活性构象与非活性构象的N-H替换为C-Me,对甲基进行力场优化,分别得到化合物2的活性与非活性构象。
2.3 用FreeForm进行张力能计算
FreeForm默认采用MMFF94S力场,此外还支持mmff94以及Open Force Field力场,包括如下几个版本:smirnoff99frosst、parsley_openff1.0.0、parsley_openff1.1.1、parsley_openff1.2.1、 parsley_openff1.3.1(最新的FreeForm还支持sage_openff2.0.0,本文没有呈现数据)。在本文中,用MMFF94S以及6个不同的Open Force Field分别对化合物1、2的活性与非活性构象进行了张力能计算。除了力场之外,所有的参数均采用默认值。
2.4 结果
不同力场对化合物1、2活性与非活性构象张力能计算的结果见表1-6。
表1.用MMFF94S力场计算化合物1、2的张力能
| Items | 1-active | 1-inactive | 2-active | 2-inactive |
|---|---|---|---|---|
| Relaxed Bioactive ΔG | 4.40 | 8.46 | 2.59 | 3.93 |
| Local ΔH | 0.15 | 0.20 | 0.80 | 1.03 |
| Global ΔE | 4.55 | 8.66 | 3.39 | 4.95 |
单位:kcal/mol
表2.用smirnoff99frosst力场计算化合物1、2的张力能
| Items | 1-active | 1-inactive | 2-active | 2-inactive |
|---|---|---|---|---|
| Relaxed Bioactive ΔG | 2.74 | 4.24 | 2.57 | 3.15 |
| Local ΔH | 1.24 | 2.25 | 3.24 | 3.65 |
| Global ΔE | 3.99 | 6.48 | 5.82 | 6.81 |
单位:kcal/mol
表3.用parsley_openff1.0.0力场计算化合物1、2的张力能
| Items | 1-active | 1-inactive | 2-active | 2-inactive |
|---|---|---|---|---|
| Relaxed Bioactive ΔG | 2.52 | 3.82 | 1.69 | 1.67 |
| Local ΔH | 0.71 | 1.09 | 1.56 | 2.24 |
| Global ΔE | 3.23 | 4.91 | 3.26 | 3.91 |
单位:kcal/mol
表4.用parsley_openff1.1.1力场计算化合物1、2的张力能
| Items | 1-active | 1-inactive | 2-active | 2-inactive |
|---|---|---|---|---|
| Relaxed Bioactive ΔG | 2.72 | 3.88 | 1.70 | 1.78 |
| Local ΔH | 0.68 | 1.02 | 1.52 | 2.01 |
| Global ΔE | 3.40 | 4.90 | 3.22 | 3.79 |
单位:kcal/mol
表5.用parsley_openff1.2.1力场计算化合物1、2的张力能
| Items | 1-active | 1-inactive | 2-active | 2-inactive |
|---|---|---|---|---|
| Relaxed Bioactive ΔG | 3.57 | 4.66 | 2.74 | 2.32 |
| Local ΔH | 0.78 | 1.43 | 1.56 | 2.6 |
| Global ΔE | 4.35 | 6.09 | 4.30 | 4.92 |
单位:kcal/mol
表6.用parsley_openff1.3.1力场计算化合物1、2的张力能
| Items | 1-active | 1-inactive | 2-active | 2-inactive |
|---|---|---|---|---|
| Relaxed Bioactive ΔG | 4.19 | 5.31 | 3.47 | 3.81 |
| Local ΔH | 0.15 | 0.39 | 0.77 | 0.85 |
| Global ΔE | 4.34 | 5.69 | 4.24 | 4.66 |
单位:kcal/mol
不同力场计算的化合物1、2的非活性构象与活性构象的全局张力能差(ΔΔE)可表示为:
ΔΔE = Global ΔEinactive – Global ΔEactive
如果ΔΔE为正值,该值越大,则表示活性构象的占比越大,对活性与JAK3的选择性均有利;反之ΔΔE越小,表示活性构象的占比越小,对活性与JAK3的选择性不利。不同力场计算的化合物1(蓝色)、2(黄色)的ΔΔE如图6所示。
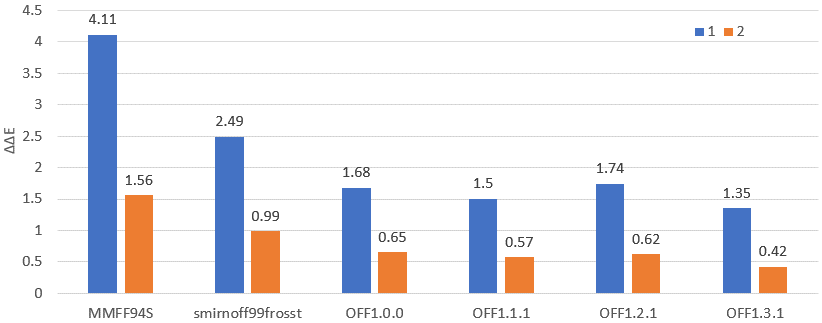
图6. 不同力场计算化合物1、2的非活性构象与活性构象的全局张力能差(ΔΔE, 单位:kcal/mol)
从图6可知:无论用哪一个力场进行计算,化合物1的ΔΔE均大于0,且比化合物2的ΔΔE要大的多,这与之前报道的QM计算结果一致,可以用来解释为什么化合物1比化合物2的活性强。但是,也注意到,与QM方法相比,力场计算的化合物2的ΔΔE偏高。尤其是MMFF94s计算的ΔΔE=1.56,偏高的太多,当然这种偏高只是相对QM计算而言。相比之下,parsley_openff系列力场计算化合物2的结果更加合理,ΔΔE更加趋近于0,尤其是OpenFF1.1.1与1.3.1与QM计算的结果更加接近。总的来说,FreeForm计算的结果可以解释化合物1、2在活性上的差异。
3. 算例2:PTP1B抑制剂
3.1 算例介绍
蛋白酪氨酸磷酸酶 1B (Protein tyrosine phosphatase 1B,PTP1B) 是胰岛素和瘦素受体通路的负调控因子(negative regulator),是糖尿病和肥胖症非常有吸引力的治疗靶标。惠氏公司的Wilson等人[6]从一个微摩尔活性水平的先导化合物开始,通过将分子从酶活性位点延伸到第二个磷酸酪氨酸结合位点来对新型PTP1B抑制剂进行基于结构的优化,在复合物共晶结构和分子模型的指导下,高效地发现了低纳摩尔的PTP1B抑制剂。该系列化合物被可被主动转运到肝细胞中,这种对靶组织的主动摄取可能是克服 PTP1B 抑制剂膜通透性差的可能途径之一。在Wilson等人[6]的研究中,涉及一对化合物3、4(结构式如图7所示),它们仅存在一个溴原子的差异,但是对PTP1B的活性(Ki)差异却高达500倍。
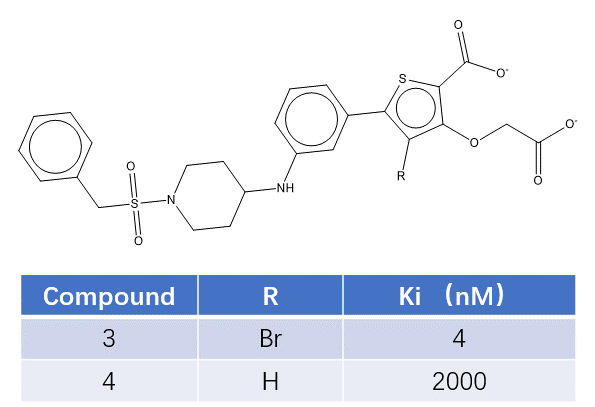
图7. 化合物3、4及其对PTP1B的活性
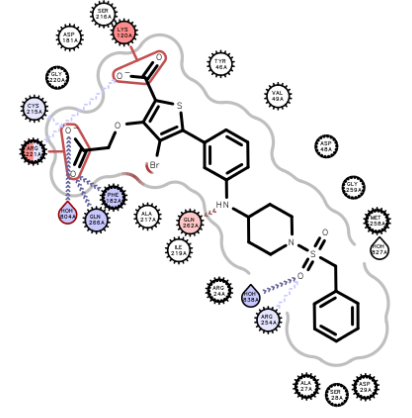
用OEChem Tk[7]分析化合物3与PTP1B的相互作用,结果如图8所示,除了Br与GLN262发生立体碰撞之外,没法发现特别的相互作用。
图8. 根据化合物3与PTP1B共晶结构PDB 2QBP分析的相互作用
用Vina 1.2分别对化合物3、4进行打分,结果如表7所示。
表7. 用AutoDock Vina打分函数预测化合物3与4的结合亲和力
| Comp. | Vina Score(kcal/mol) | Gauss 1 | Gauss 2 | repulsion | Hydrophobic | H-Bond |
|---|---|---|---|---|---|---|
| 3 | -8.80 | 112.13449 | 1790.27698 | 3.73331 | 37.84272 | 4.30573 |
| 4 | -9.06 | 106.32247 | 1727.02248 | 2.58149 | 37.20075 | 4.30573 |
注:本次计算蛋白结构从PDB 2QBP准备而来,并删除全部水分子。
可以发现,化合物3与4的疏水、氢键相互作用项贡献相同;比起化合物4,化合物3的Br原子与GLN262发生立体碰撞具有更大的排斥项,因此3预测的结合亲和力还比4略差。因此,经典AutoDock Vina分子对接不能通过分子间相互作用来解释化合物3、4在活性上的差异。
根据前期QM分析(未呈现),我们认为Br主要通过空间立体位阻效应而稳定其邻位的氧乙酸侧链构象,从而对相互作用有利;相比之下,化合物4由于没有Br的稳定构象作用,氧乙酸侧链不容易保持其相互作用有利的构象,因此活性更低。由此可以预期,化合物3比4具有更低构象张力能。
3.2 结构准备
化合物3从Wilson等人[6]解释的共晶结构PDB 2QBP提取,化合物4的结构是将3的Br修改为H并对仅H优化后而得,假设化合物3与4具有共同的结合模式。
3.3 用FreeForm进行张力能计算
采用MMFF94S、smirnoff99frosst、parsley_openff1.0.0、parsley_openff1.1.1、parsley_openff1.2.1、parsley_openff1.3.1等力场对化合物3、4的进行全局张力能计算,所有的其它参数均采用默认值。
3.4 结果
不同力场对化合物3、4活性构象张力能计算的结果见表8-13。
表8. 用MMFF94S力场计算化合物3、4的张力能
| Items | 3 | 4 |
|---|---|---|
| Relaxed Bioactive ΔG | 4.38 | 5.52 |
| Local ΔH | 6.49 | 6.39 |
| Global ΔE | 10.87 | 11.91 |
单位:kcal/mol
表9. 用smirnoff99frosst力场计算化合物3、4的张力能
| Items | 3 | 4 |
|---|---|---|
| Relaxed Bioactive ΔG | 6.60 | 7.09 |
| Local ΔH | 3.23 | 4.76 |
| Global ΔE | 9.83 | 11.86 |
单位:kcal/mol
表10. 用parsley_openff1.0.0力场计算化合物3、4的张力能
| Items | 3 | 4 |
|---|---|---|
| Relaxed Bioactive ΔG | 2.97 | 2.92 |
| Local ΔH | 3.20 | 4.41 |
| Global ΔE | 6.17 | 7.32 |
单位:kcal/mol
表11. 用parsley_openff1.1.1力场计算化合物3、4的张力能
| Items | 3 | 4 |
|---|---|---|
| Relaxed Bioactive ΔG | 3.10 | 3.23 |
| Local ΔH | 3.24 | 4.39 |
| Global ΔE | 6.34 | 7.62 |
单位:kcal/mol
表12. 用parsley_openff1.2.1力场计算化合物3、4的张力能
| Items | 3 | 4 |
|---|---|---|
| Relaxed Bioactive ΔG | 2.80 | 3.02 |
| Local ΔH | 2.92 | 4.75 |
| Global ΔE | 5.72 | 7.77 |
单位:kcal/mol
表13. 用parsley_openff1.3.1力场计算化合物3、4的张力能
| Items | 3 | 4 |
|---|---|---|
| Relaxed Bioactive ΔG | 3.20 | 2.96 |
| Local ΔH | 3.86 | 7.26 |
| Global ΔE | 7.06 | 10.22 |
单位:kcal/mol
从表8-13可以发现,不同力场计算的化合物3全局张力能总比化合物4的低,这与我们的预期一致:化合物3的Br通过空间位阻稳定了氧乙酸侧链的构象。从parsley_openff1.3.1计算的结果(表13)可以发现,化合物3在构象自由能(Relaxed Bioactive ΔG)上并没有比4更低,但是3在local ΔH上比4占有绝对优势,这主要得益于Br的空间位阻。
为了更加直观、方便的比较两者的张力能,引入化合物3、4全局张力能差(ΔΔE):
ΔΔE = Global ΔE4 – Global ΔE3
不同力场计算的化合物3、的ΔΔE如图9所示。
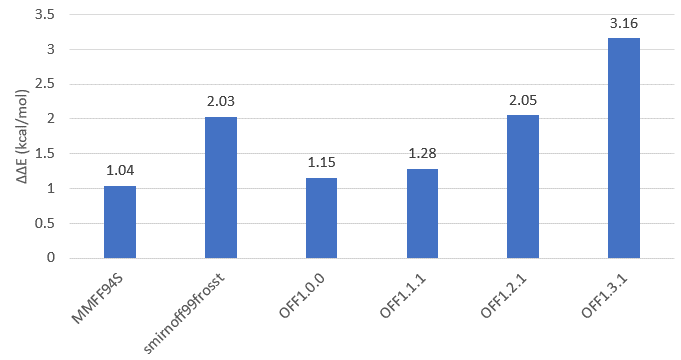
图9. 不同力场计算化合物3、4的全局张力能差(ΔΔE, 单位:kcal/mol)
总的来说,如图9所示,不管那个力场,都给出了预期的化合物4比3具有更高的张力能(ΔΔE大于0),FreeForm计算的张力能给出了正确的排序。但也注意到,不同的力场给出的张力能相差相当大,目前的测试并不清楚哪个力场会表现更好,需要更多的数据进行测试。
3. 小结
本文用两对化学结构仅一个原子差异但活性相差巨大的分子对为例,尝试用FreeForm以不同的力场计算张力能用以解释活性差异的原因。第1个算例来自JAK3共价抑制剂,化合物具有活性与非活性两种潜在构象,freeform可以正确地对活性与非活性构象的张力能进行排序,并解释活性差异的原因。第2个算例为一对溴代与脱溴的PTP1B抑制剂,其活性差异主要源于Br的立体位阻,freeform的张力能可以正确地对这一对化合物的活性进行排序,并解释活性差异原因,这可以弥补分子对接打分函数与相互作用分析的不足。
在两个算例中,不管用哪个力场,都对化合物的张力能做出了正确判断。不同的力场计算的张力能在数值上的差异也相当大,哪个力场更好、更具普适性需要更多的算例进行验证。但是无论如何,FreeForm提供了多种力场选择以应对不同的场景。
4. 相关主题
- 文献重现|大环EGFR激酶抑制剂BI-4020的先导化合物5与6的发现与设计
- OpenEye案例 | 用FreeForm改善MM/PBSA计算结合自由能
- FreeForm–构象稳定性评估及其在先导化合物优化中的应用
5. 文献
- 肖高铿. FreeForm–构象稳定性评估及其在先导化合物优化中的应用. 墨灵格的博客. 2016-07-02. http://blog.molcalx.com.cn/2016/07/02/freeform-conformer-stability.html
- 肖高铿. 用FreeForm改善MM/PBSA计算结合自由能. 墨灵格的博客. 2019-06-05. http://blog.molcalx.com.cn/2019/06/05/openeye-freeform-mmpbsa.html
- Thorarensen, A.; et al. Design of a Janus Kinase 3 (JAK3) Specific Inhibitor 1-((2 S ,5 R )-5-((7 H -Pyrrolo[2,3- d ]Pyrimidin-4-Yl)Amino)-2-Methylpiperidin-1-Yl)Prop-2-En-1-One (PF-06651600) Allowing for the Interrogation of JAK3 Signaling in Humans. J. Med. Chem. 2017, 60 (5), 1971–1993. https://doi.org/10.1021/acs.jmedchem.6b01694.
- 肖高铿. 选择性JAK3抑制剂PF-06651600的设计. 墨灵格的博客. 2019-11-10. http://blog.molcalx.com.cn/2019/11/10/jak3-inhibiotr-pf-06651600.html
- 肖高铿. 势能面扫描在Torsion Profile中的应用. 墨灵格的博客. 2020-01-30. http://blog.molcalx.com.cn/2020/01/30/qm-torsion-profile.html#JAK3
- Wilson, D. P.; Wan, Z.-K.; Xu, W.-X.; Kirincich, S. J.; Follows, B. C.; Joseph-McCarthy, D.; Foreman, K.; Moretto, A.; Wu, J.; Zhu, M.; et al. Structure-Based Optimization of Protein Tyrosine Phosphatase 1B Inhibitors: From the Active Site to the Second Phosphotyrosine Binding Site. J. Med. Chem. 2007, 50 (19), 4681–4698. https://doi.org/10.1021/jm0702478.
- OEChemTk. https://www.eyesopen.com/oechem-tk